题目内容
已知a1=1,an=an-1+3n-1,求数列{an}的通项公式an.
考点:数列递推式
专题:计算题,等差数列与等比数列
分析:利用递推关系一步步地把通项用首项和关于n的表达式表示出来,即可求得an.
解答:
解:由题得,an=an-1+3n-1=an-2+3n-2+3n-1=an-3+2n-3+3n-2+3n-1
=…=a1+31+32+…+3n-1=1+
=-
+
×3n.
=…=a1+31+32+…+3n-1=1+
| 3(1-3n-1) |
| 1-3 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题是对递推关系式和等比数列求和公式的综合考查.比较基础.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
若a,b,c是等比数列,则下列不一定是等比数列的项的是( )
| A、a2,b2,c2 | ||||||
| B、a+2,b+2,c+2 | ||||||
C、
| ||||||
| D、2a,2b,2c |
某小朋友用手指按如图所示的规则练习数数,数到2009时对应的指头是( )


| A、大拇指 | B、食指 |
| C、中指 | D、无名指 |
在极坐标系中,圆ρ=4cosθ的垂直于极轴的两条切线方程分别为( )
| A、θ=0(ρ∈R)和ρcosθ=4 | ||
B、θ=
| ||
| C、θ=0(ρ∈R)和ρcosθ=2 | ||
D、θ=
|
(x-1)5的展开式中,x3的系数为 ( )
| A、-10 | B、-5 | C、5 | D、10 |
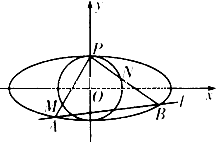 如图,椭圆C:
如图,椭圆C: