题目内容
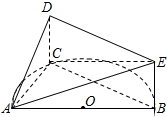 如图,AB是半圆O的直径,C是半圆O上除A、B外的一个动点,DC⊥平面ABC,DC∥BE,CD=BE,AB=4,tan∠EAB=
如图,AB是半圆O的直径,C是半圆O上除A、B外的一个动点,DC⊥平面ABC,DC∥BE,CD=BE,AB=4,tan∠EAB=| 1 |
| 4 |
(1)证明:平面ADE⊥平面ACD;
(2)试探究当C在什么位置时三棱锥C-ADE的体积取得最大值,请说明理由并求出这个最大值.
考点:平面与平面垂直的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)由已知条件推导出四边形BCDE是平行四边形,由此能证明平面ADE⊥平面ACD.
(2)当C为半圆弧中点时三棱锥C-ADE的体积取得最大值,最大值为
.
(2)当C为半圆弧中点时三棱锥C-ADE的体积取得最大值,最大值为
| 4 |
| 3 |
解答:
(1)证明:因为AB是直径,所以BC⊥AC,
因为CD⊥平面ABC,CD⊥BC,
因为CD∩AC=C,所以BC⊥平面ACD
 因为CD∥BE,又因为CD=BE,
因为CD∥BE,又因为CD=BE,
所以四边形BCDE是平行四边形,
所以BC∥DE,所以DE⊥平面ACD,
因为DE?平面ADE,所以平面ADE⊥平面ACD.
(2)解:依题意,EB=AB×tan∠EAB=4×
=1,
由(1)知VC-ADE=VE-ACD=
×S△ACD×DE
=
×
×AC×CD×DE
=
×AC×BC
≤
×(AC2+BC2)=
×AB2=
,
等号当且仅当AC=BC=2
时成立,
所以当C为半圆弧中点时三棱锥C-ADE的
体积取得最大值,最大值为
.
此时,AD=
=3,S△ADE=
×AD×DE=3
,
设三棱锥C-ADE的高为h,
则VC-ADE=
×S△ADE×h=
,h=
.
因为CD⊥平面ABC,CD⊥BC,
因为CD∩AC=C,所以BC⊥平面ACD
 因为CD∥BE,又因为CD=BE,
因为CD∥BE,又因为CD=BE,所以四边形BCDE是平行四边形,
所以BC∥DE,所以DE⊥平面ACD,
因为DE?平面ADE,所以平面ADE⊥平面ACD.
(2)解:依题意,EB=AB×tan∠EAB=4×
| 1 |
| 4 |
由(1)知VC-ADE=VE-ACD=
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
=
| 1 |
| 6 |
≤
| 1 |
| 12 |
| 1 |
| 12 |
| 4 |
| 3 |
等号当且仅当AC=BC=2
| 2 |
所以当C为半圆弧中点时三棱锥C-ADE的
体积取得最大值,最大值为
| 4 |
| 3 |
此时,AD=
12+(2
|
| 1 |
| 2 |
| 2 |
设三棱锥C-ADE的高为h,
则VC-ADE=
| 1 |
| 3 |
| 4 |
| 3 |
2
| ||
| 3 |
点评:本题考查平面与平面垂直的证明,考查三棱锥体积的最大值的求法,解题时要认真审题,注意空间思维能力的合理运用.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
动点A到定点F1(0,-2)和F2(0,2)的距离和为4,则点A的轨迹为( )
| A、椭圆 | B、线段 |
| C、无轨迹 | D、两条射线 |
y=cosx•sinx是( )
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数也是偶函数 |
| D、既不是奇函数也不是偶函数 |
函数函数f(x)=x2-4x+5-2lnx的零点个数为( )
| A、3 | B、2 | C、1 | D、0 |
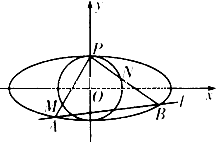 如图,椭圆C:
如图,椭圆C: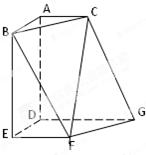 如图,在多面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,BA⊥AC,ED⊥DG,EF∥DG且AC=1,AB=ED=EF=2,AD=DG=4.
如图,在多面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,BA⊥AC,ED⊥DG,EF∥DG且AC=1,AB=ED=EF=2,AD=DG=4.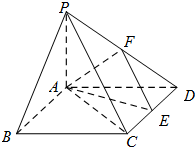 如图在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=
如图在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB= 如图,已知正方体ABCD-A1B1C1D1的棱长为2,M为正方形AA1D1D的中心,N为棱AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,M为正方形AA1D1D的中心,N为棱AB的中点.