题目内容
某校一社团共有10名成员,从周一到周五每天安排两人值日,若甲、乙必须排在同一天,且丙、丁不能排在同一天,则不同的安排方案共有( )
| A、21600 | B、10800 |
| C、7200 | D、5400 |
考点:计数原理的应用
专题:排列组合
分析:本题需要三步完成这件事情,第一步安排,甲乙,丙,丁,第二步给丙,丁个补充1人,第三步,再安排剩余的4人,根据分步计数可得.
解答:
解:由题意,从5天中任排三天给甲乙,丙,丁有
种;
其他六人抽出两人为丙丁各安排一人,有
种;
剩下四人值两天班,有
种;
根据分步计数原理可得,
•
•
=10800种.
故选:B.
| A | 3 5 |
其他六人抽出两人为丙丁各安排一人,有
| A | 2 6 |
剩下四人值两天班,有
| C | 2 4 |
根据分步计数原理可得,
| A | 3 5 |
| A | 2 6 |
| C | 2 4 |
故选:B.
点评:本题主要考查了分布计数原理,合理分步是关键,属于中档题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
运行如图所示的程序,如果输出结果为sum=1320,那么判断框中应填( )


| A、i≥9 | B、i≥10 |
| C、i≤9 | D、i≤10 |
若a,b,c是等比数列,则下列不一定是等比数列的项的是( )
| A、a2,b2,c2 | ||||||
| B、a+2,b+2,c+2 | ||||||
C、
| ||||||
| D、2a,2b,2c |
动点A到定点F1(0,-2)和F2(0,2)的距离和为4,则点A的轨迹为( )
| A、椭圆 | B、线段 |
| C、无轨迹 | D、两条射线 |
若函数f(x)=x3-x2+a在[-1,1]的最小值是1,则实数a的值是( )
| A、1 | ||
| B、3 | ||
C、
| ||
| D、-1 |
已知{an}是等比数列,a4•a7=-512,a3+a8=124,且公比为整数,则公比q为( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
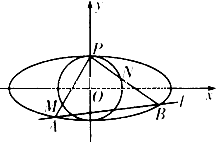 如图,椭圆C:
如图,椭圆C: