题目内容
 如图,设A是单位圆和x轴正半轴的交点,P、Q是单位圆上的两点O是坐标原点,∠AOP=
如图,设A是单位圆和x轴正半轴的交点,P、Q是单位圆上的两点O是坐标原点,∠AOP=| π |
| 6 |
(Ⅰ)求P点坐标;
(Ⅱ)若Q(
| 3 |
| 5 |
| 4 |
| 5 |
| π |
| 6 |
考点:两角和与差的余弦函数,任意角的三角函数的定义
专题:三角函数的求值
分析:(Ⅰ)设P(x,y)则由题意可得 x=cos
=
,y=sin
=
,可得点P的坐标.
(II)由Q的坐标求得sinα=
,cosα=
.根据cos(α-
)=cosαsin
+sinαcos
,计算求得结果.
| π |
| 6 |
| ||
| 2 |
| π |
| 6 |
| 1 |
| 2 |
(II)由Q的坐标求得sinα=
| 4 |
| 5 |
| 3 |
| 5 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
解答:
解:(Ⅰ)设P(x,y)则由题意可得 x=cos
=
,y=sin
=
,
所以P(
,
).
(II)因为Q(
,
),所以sinα=
,cosα=
.
∴cos(α-
)=cosαsin
+sinαcos
=
×
+
×
=
.
| π |
| 6 |
| ||
| 2 |
| π |
| 6 |
| 1 |
| 2 |
所以P(
| ||
| 2 |
| 1 |
| 2 |
(II)因为Q(
| 3 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
∴cos(α-
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 3 |
| 5 |
| ||
| 2 |
| 4 |
| 5 |
| 1 |
| 2 |
3
| ||
| 10 |
点评:本题主要考查任意角的三角函数的定义、两角差的余弦公式的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将长为L的木棒随机折成3段,则3段构成三角形的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
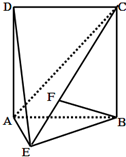 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.