题目内容
设函数f（x）=sinx+
cosx，x∈R．
（1）求f（x）最小正周期；
（2）求f（x）的最大值及相应的x值；
（3）用五点法画出函数f（x）在一个周期内的图象（要求列表描点作图）．
| 3 |
（1）求f（x）最小正周期；
（2）求f（x）的最大值及相应的x值；
（3）用五点法画出函数f（x）在一个周期内的图象（要求列表描点作图）．
考点：两角和与差的正弦函数,三角函数的周期性及其求法,五点法作函数y=Asin（ωx+φ）的图象
专题：三角函数的图像与性质
分析：（1）化简函数的解析式为f（x）=2sin（x+
），可得函数的周期为2π．
（2）令 x+
=2kπ+
，k∈z，可得f（x）的最大值为2，求得此时x的值．
（3）用五点法作出函数在一个周期内的简图．
| π |
| 3 |
（2）令 x+
| π |
| 3 |
| π |
| 2 |
（3）用五点法作出函数在一个周期内的简图．
解答：
解：（1）∵函数f（x）=sinx+
cosx=2（
sinx+
cosx）=2sin（x+
），故函数的周期为2π．
（2）令 x+
=2kπ+
，k∈z，可得f（x）的最大值为2，此时，x=2kπ+
，k∈z．
（3）列表：
作图：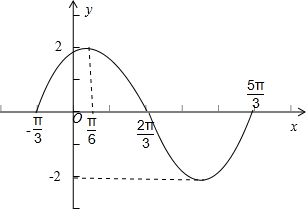
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
（2）令 x+
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
（3）列表：
x+
|
0 |
|
π |
|
2π | ||||||||||
| x | -
|
|
|
|
| ||||||||||
| y | 0 | 2 | 0 | -2 | 0 |
点评：本题主要考查两角和差的正弦公式，正弦函数的最值，用五点法作函数y=Asin（ωx+φ）的图象，属于中档题．
练习册系列答案
相关题目
直线y=5与y=-1在区间[0，π]上截曲线y=Asin2x+B（A＞0，B＞0）所得的线段长相等且不为0，则下列描述正确的是（ ）
A、A≤
| ||||
| B、A≤3，B=2 | ||||
C、A＞
| ||||
| D、A＞3，B=2 |
如图所示，用篱笆围成一个一边靠墙的矩形菜园，假设墙有足够长．
如图，设A是单位圆和x轴正半轴的交点，P、Q是单位圆上的两点O是坐标原点，∠AOP=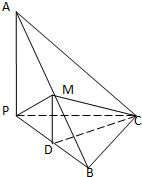
如图，已知三棱锥A-PBC中，AC⊥BC，AP⊥PC，M为AB的中点，D为PB的中点，且△PMB为正三角形．