题目内容
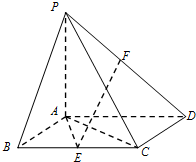 如图,已知四棱锥P-ABCD,底面ABCD为边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点,PA=AB.
如图,已知四棱锥P-ABCD,底面ABCD为边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点,PA=AB.(Ⅰ)证明:AE⊥PD;
(Ⅱ)若F为PD上的动点,求EF与平面PAD所成最大角的正切值.
考点:直线与平面所成的角
专题:空间位置关系与距离
分析:(Ⅰ)由题设条件知△ABC为正三角形,先推导出AE⊥AD,PA⊥AE,由直线垂直于平面的判定定理得到AE⊥平面PAD,由此能证明AE⊥PD.
(Ⅱ)连结AF,则∠AFE为EF与平面PAD所成的角,当AF⊥PD时,∠AFE最大,由此能求出EF与平面PAD所成最大角的正切值.
(Ⅱ)连结AF,则∠AFE为EF与平面PAD所成的角,当AF⊥PD时,∠AFE最大,由此能求出EF与平面PAD所成最大角的正切值.
解答:
 解:(Ⅰ)因为四边形ABCD为菱形,且∠ABC=60°,
解:(Ⅰ)因为四边形ABCD为菱形,且∠ABC=60°,
所以△ABC为正三角形.
E为BC中点,故AE⊥BC;
又因为AD∥BC,所以AE⊥AD.…(3分)
因为PA⊥平面ABCD,AE?平面ABCD,
所以PA⊥AE.…(5分)
故AE⊥平面PAD,又PD?平面PAD,
所以AE⊥PD.…(7分)
(Ⅱ)连结AF,由(Ⅰ)知AE⊥平面PAD,
所以∠AFE为EF与平面PAD所成的角.…(10分)
在Rt△AEF中,AE=
,∠AFE最大当且仅当AF最短,
即AF⊥PD时,∠AFE最大.…(12分)
依题意,此时,在Rt△PAD中,PA•AD=PD•AF,
所以AF=
,tan∠AFE=
=
.
所以,EF与平面PAD所成最大角的正切值为
.…(15分)
 解:(Ⅰ)因为四边形ABCD为菱形,且∠ABC=60°,
解:(Ⅰ)因为四边形ABCD为菱形,且∠ABC=60°,所以△ABC为正三角形.
E为BC中点,故AE⊥BC;
又因为AD∥BC,所以AE⊥AD.…(3分)
因为PA⊥平面ABCD,AE?平面ABCD,
所以PA⊥AE.…(5分)
故AE⊥平面PAD,又PD?平面PAD,
所以AE⊥PD.…(7分)
(Ⅱ)连结AF,由(Ⅰ)知AE⊥平面PAD,
所以∠AFE为EF与平面PAD所成的角.…(10分)
在Rt△AEF中,AE=
| 3 |
即AF⊥PD时,∠AFE最大.…(12分)
依题意,此时,在Rt△PAD中,PA•AD=PD•AF,
所以AF=
| 2 |
| AE |
| AF |
| ||
| 2 |
所以,EF与平面PAD所成最大角的正切值为
| ||
| 2 |
点评:本题考查异面直线垂直的证明,考查直线与平面所成最大角的正切值的求法,解题时要注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
命题p:不等式
<0的解集为{x|0<x<1},命题q:“α=β”是“sinα=sinβ”成立的必要不充分条件,则( )
| x |
| x-1 |
| A、p真q假 |
| B、“p且q”为真 |
| C、“p或q”为假 |
| D、p假q真 |
