题目内容
设函数f(x,n)=(1+x)n,(n∈N*).
(1)求f(x,6)的展开式中系数最大的项;
(2)若f(i,n)=32i(i为虚数单位),求C
-C
+C
-C
+C
.
(1)求f(x,6)的展开式中系数最大的项;
(2)若f(i,n)=32i(i为虚数单位),求C
1 n |
3 n |
5 n |
7 n |
9 n |
考点:二项式定理的应用
专题:计算题,二项式定理
分析:(1)展开式中系数最大的项是第4项;
(2)(1+i)n=32i,两边取模,求出n,利用(1+x)10=(
-
+
-
+
-
+(
-
+
-
+
)i=32i,可得结论.
(2)(1+i)n=32i,两边取模,求出n,利用(1+x)10=(
| C | 0 10 |
| C | 2 10 |
| C | 4 10 |
| C | 6 10 |
| C | 8 10 |
| C | 10 10 |
| C | 1 10 |
| C | 3 10 |
| C | 5 10 |
| C | 7 10 |
| C | 9 10 |
解答:
解:(1)展开式中系数最大的项是第4项=
(x)3=20x3;…5′
(2)由已知,(1+i)n=32i,两边取模,得(
)n=32,所以n=10.
所以C
-C
+C
-C
+C
=
-
+
-
+
,
而(1+x)10=(
-
+
-
+
-
+(
-
+
-
+
)i=32i
所以
-
+
-
+
=32.
| C | 3 6 |
(2)由已知,(1+i)n=32i,两边取模,得(
| 2 |
所以C
1 n |
3 n |
5 n |
7 n |
9 n |
| C | 1 10 |
| C | 3 10 |
| C | 5 10 |
| C | 7 10 |
| C | 9 10 |
而(1+x)10=(
| C | 0 10 |
| C | 2 10 |
| C | 4 10 |
| C | 6 10 |
| C | 8 10 |
| C | 10 10 |
| C | 1 10 |
| C | 3 10 |
| C | 5 10 |
| C | 7 10 |
| C | 9 10 |
所以
| C | 1 10 |
| C | 3 10 |
| C | 5 10 |
| C | 7 10 |
| C | 9 10 |
点评:本题考查二项式定理的运用,考查学生分析解决问题的能力,考查复数的运算,属于中档题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
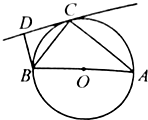 如图,⊙O的直径AB=4,C为圆周上一点,AC=3,CD是⊙O的切线,BD⊥CD于D,则CD=
如图,⊙O的直径AB=4,C为圆周上一点,AC=3,CD是⊙O的切线,BD⊥CD于D,则CD=