题目内容
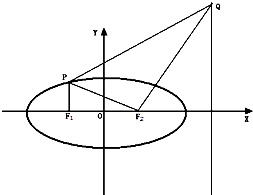 如图,点F1(-c,0)、F2(c,0)分别是椭圆
如图,点F1(-c,0)、F2(c,0)分别是椭圆C:
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| c |
(1)如果点Q的坐标为(4,4),求椭圆C的方程;
(2)试判断直线PQ与椭圆C的公共点个数,并证明你的结论.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)先求得P点的坐标,根据PF2⊥QF2,可得QF2的方程,将x=
代入,结合点Q的坐标为(4,4),即可求椭圆C的方程;
(2)求出直线PQ的方程,代入椭圆C的方程,求出方程的解,即可得出结论.
| a2 |
| c |
(2)求出直线PQ的方程,代入椭圆C的方程,求出方程的解,即可得出结论.
解答:
 解:(1)解方程组
解:(1)解方程组
得P点的坐标为(-c,
),
∴kPF2=
=-
,
∵PF2⊥QF2,
∴kQF2=
,
∴QF2的方程为:y=
(x-c)
将x=
代入上式解得y=2a,
∴Q点的坐标为(
,2a);
∵Q点的坐标为(4,4),∴
=4且2a=4,
∴a=2,c=1,b2=a2-c2=3,
∴椭圆C的方程为
+
=1;
(2)∵Q点的坐标为(
,2a),P点的坐标为(-c,
),
∴kPQ=
=
=
,
∴PQ的方程为y-2a=
(x-
),
即y=
x+a
将PQ的方程代入椭圆C的方程得b2x2+a2(
x+a)2=a2b2,
∴(b2+c2)x2+2a2cx+a4-a2b2=0①
∵a2=b2+c2
∴方程①可化为a2x2+2a2cx+a2c2=0
解得x=-c
∴直线PQ与椭圆C只有一个公共点.
 解:(1)解方程组
解:(1)解方程组
|
| b2 |
| a |
∴kPF2=
| ||
| -c-c |
| b2 |
| 2ac |
∵PF2⊥QF2,
∴kQF2=
| 2ac |
| b2 |
∴QF2的方程为:y=
| 2ac |
| b2 |
将x=
| a2 |
| c |
∴Q点的坐标为(
| a2 |
| c |
∵Q点的坐标为(4,4),∴
| a2 |
| c |
∴a=2,c=1,b2=a2-c2=3,
∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)∵Q点的坐标为(
| a2 |
| c |
| b2 |
| a |
∴kPQ=
2a-
| ||
|
| c(2a2-b2) |
| a(a2+c2) |
| c |
| a |
∴PQ的方程为y-2a=
| c |
| a |
| a2 |
| c |
即y=
| c |
| a |
将PQ的方程代入椭圆C的方程得b2x2+a2(
| c |
| a |
∴(b2+c2)x2+2a2cx+a4-a2b2=0①
∵a2=b2+c2
∴方程①可化为a2x2+2a2cx+a2c2=0
解得x=-c
∴直线PQ与椭圆C只有一个公共点.
点评:本题考查椭圆的方程,考查直线与椭圆的位置关系,考查直线的方程,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
在五个数字1,2,3,4,5中,若随机取出三个数字,则剩下两个数字的和是奇数的概率是( )
| A、0.3 | B、0.4 |
| C、0.5 | D、0.6 |
下列说法正确的是( )
| A、若已知两个变量具有线性相关关系,且它们正相关,则其线性回归直线的斜率为正 |
| B、直线l垂直于平面α的充要条件为l垂直于平面α内的无数条直线 |
| C、若随机变量ξ~N(10,0.12),且P(9.9<ξ<10.1)=0.6826,则P(ξ>10.1)=0.3174 |
| D、已知命题P:?x∈R,x2-2x+2>0,则¬p:?x∈R,x2-2x+2<0 |
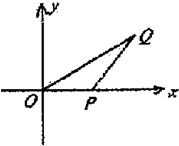 如图已知△OPQ的面积为S,且
如图已知△OPQ的面积为S,且