题目内容
当a=4或a≤0时,不等式x2-6x<a(x-2)恒成立,求x的取值范围.
考点:函数恒成立问题,二次函数的性质
专题:函数的性质及应用
分析:先构造函数f(a)=a(x-2)-x2+6x,以a为主元,再解一元二次不等式即可
解答:
解:构造函数f(a)=a(x-2)-x2+6x,使得函数在a=4或a≤0时,函数值恒大于0,
则由题意
,
∴
,
解得0<x<5-
.
∴x的取值范围:(0,5-
).
则由题意
|
∴
|
解得0<x<5-
| 17 |
∴x的取值范围:(0,5-
| 17 |
点评:本题的考点是函数恒成立问题的应用,一元二次不等式的解法,主要考查解一元二次不等式,关键是变换主元,考查学生等价转化问题的能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
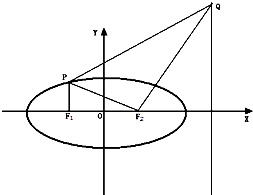 如图,点F1(-c,0)、F2(c,0)分别是椭圆
如图,点F1(-c,0)、F2(c,0)分别是椭圆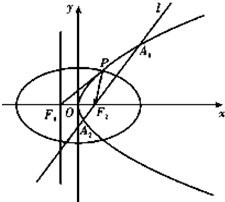 如图,设抛物线
如图,设抛物线