题目内容
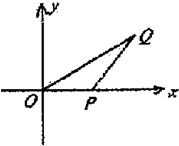 如图已知△OPQ的面积为S,且
如图已知△OPQ的面积为S,且| OP |
| PQ |
(1)若S∈(
| 1 |
| 2 |
| ||
| 2 |
(2)设|
| OP |
| 3 |
| 4 |
| OQ |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)设
与
的夹角为θ,则
与
的夹角为π-θ,根据S=
•
tanθ,以及
•
=1,S∈(
,
)求得tanθ的范围,可得θ的范围.
(II)设Q(x0,y0),根据条件求得y0和x0的值,可得|
|的解析式.令f(x)=x+
,根据它的单调性可得|
|的最小值为
,可得焦点坐标,再利用椭圆的定义求得a,再根据椭圆的性质求得b,从而求得椭圆的方程.
| OP |
| PQ |
| PO |
| PQ |
| 1 |
| 2 |
| OP |
| PQ |
| OP |
| PQ |
| 1 |
| 2 |
| ||
| 2 |
(II)设Q(x0,y0),根据条件求得y0和x0的值,可得|
| OQ |
| 1 |
| x |
| OQ |
| ||
| 2 |
解答:
解:(Ⅰ)设
与
的夹角为θ,则
与
的夹角为π-θ,
∵S=
|
||
|sin(π-θ)=
|
||
|sinθ=
|
||
|cosθtanθ=
•
tanθ.
又
•
=1,S∈(
,
),∴
•
tanθ∈(
,
),
∴tanθ∈(1,
),θ∈(
,
).
(II)设Q(x0,y0),则S=
m|y0|=
,∴y0=±
.
∴
=(m,0),
=(X0-m,±
).
由
•
=m(x0-m)=1,∴x0=m+
.
∴Q(m+
,±
),|
|=
.
令f(x)=x+
,则f(x)在(1,+∞)上是增函数,故f(x)在[2,+∞)上是增函数,
∴当m=2时,|
|的最小值为
=
.
此时P(2,0),椭圆的另一焦点为P′(-2,0),
则椭圆长轴长2a=|
|+|
|=
+
=2
,
∴a=
,b=
=
,
故椭圆的方程为
+
=1.
| OP |
| PQ |
| PO |
| PQ |
∵S=
| 1 |
| 2 |
| PO |
| PQ |
| 1 |
| 2 |
| PO |
| PQ |
| 1 |
| 2 |
| PO |
| PQ |
| 1 |
| 2 |
| OP |
| PQ |
又
| OP |
| PQ |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| OP |
| PQ |
| 1 |
| 2 |
| ||
| 2 |
∴tanθ∈(1,
| 3 |
| π |
| 4 |
| π |
| 3 |
(II)设Q(x0,y0),则S=
| 1 |
| 2 |
| 3m |
| 4 |
| 3 |
| 2 |
∴
| OP |
| PQ |
| 3 |
| 2 |
由
| OP |
| PQ |
| 1 |
| m |
∴Q(m+
| 1 |
| m |
| 3 |
| 2 |
| OQ |
(m+
|
令f(x)=x+
| 1 |
| x |
∴当m=2时,|
| OQ |
(2+
|
| ||
| 2 |
此时P(2,0),椭圆的另一焦点为P′(-2,0),
则椭圆长轴长2a=|
| QP |
| QP′ |
(
|
(
|
| 10 |
∴a=
| 10 |
| 10-4 |
| 6 |
故椭圆的方程为
| x2 |
| 10 |
| y2 |
| 6 |
点评:本题主要考查椭圆的定义、性质、以及标准方程的应用,两个向量坐标形式的运算,属于中档题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
已知复数方程
=i(i为虚数单位),则复数z的虚部为( )
| 1+i |
| 3i+z |
| A、2 | B、4i | C、-2 | D、-4 |
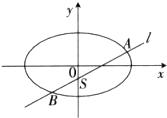 已知F1,F2是椭圆E:
已知F1,F2是椭圆E: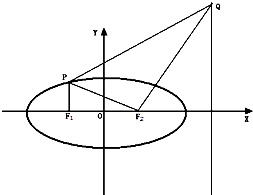 如图,点F1(-c,0)、F2(c,0)分别是椭圆
如图,点F1(-c,0)、F2(c,0)分别是椭圆