题目内容
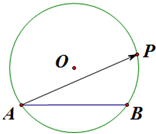
已知圆O的半径为2，圆O的一条弦AB长是3，P圆O上的任意一点，则
•
的最大值为 ．
| AB |
| AP |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：如图所示，连接OA，OB．过点O作OC⊥AB，垂足为C．利用垂径定理可得AC=
AB=
．可得cos∠OAB．利用向量的三角形法则
•
=
•(
-
)=
•
-
•
即可得出．
| 1 |
| 2 |
| 3 |
| 2 |
| AB |
| AP |
| AB |
| OP |
| OA |
| AB |
| OP |
| AB |
| OA |
解答：
解：如图所示，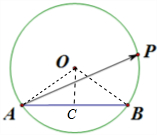
连接OA，OB．
过点O作OC⊥AB，垂足为C．
则AC=
AB=
．
∴cos∠OAB=
=
=
．
•
=
•(
-
)=
•
-
•
=|
| |
|cos＜
，
＞+3×2cos∠OAB
≤3×2×1+3×2×
=
．
当且仅当
∥
且同向时取等号．
∴
•
的最大值为
故答案为：
．
连接OA，OB．过点O作OC⊥AB，垂足为C．
则AC=
| 1 |
| 2 |
| 3 |
| 2 |
∴cos∠OAB=
| AC |
| OA |
| ||
| 2 |
| 3 |
| 4 |
| AB |
| AP |
| AB |
| OP |
| OA |
| AB |
| OP |
| AB |
| OA |
=|
| AB |
| OP |
| AB |
| OP |
≤3×2×1+3×2×
| 3 |
| 4 |
| 21 |
| 2 |
当且仅当
| OP |
| AB |
∴
| AB |
| AP |
| 21 |
| 2 |
故答案为：
| 21 |
| 2 |
点评：本题考查了向量的数量积运算、垂径定理、向量共线定理，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
如图是一个几何体的正视图、侧视图、俯视图，则该几何体的体积是