题目内容
等差数列{an}的公差d≠0，an∈R，前n项和为Sn，则对正整数m，下列四个结论中：
（1）Sm，S2m-Sm，S3m-S2m成等差数列，也可能成等比数列；
（2）Sm，S2m-Sm，S3m-S2m成等差数列，但不可能成等比数列；
（3）Sm，S2m，S3m可能成等比数列，但不可能成等差数列；
（4）Sm，S2m，S3m不可能成等比数列，也不可能成等差数列；
正确的是（ ）
（1）Sm，S2m-Sm，S3m-S2m成等差数列，也可能成等比数列；
（2）Sm，S2m-Sm，S3m-S2m成等差数列，但不可能成等比数列；
（3）Sm，S2m，S3m可能成等比数列，但不可能成等差数列；
（4）Sm，S2m，S3m不可能成等比数列，也不可能成等差数列；
正确的是（ ）
| A、（1）（3） |
| B、（1）（4） |
| C、（2）（3） |
| D、（2）（4） |
考点：等差数列的性质
专题：等差数列与等比数列
分析：由等差数列的性质可得Sm，S2m-Sm，S3m-S2m成等差数列，可知（2）正确；只有当d=0时，才有Sm，S2m，S3m成等比数列，故（4）正确，可得答案．
解答：
解：由等差数列的性质可得Sm，S2m-Sm，S3m-S2m成等差数列，
若也成等比数列，则必须有数列为常数列，与d≠0矛盾，
故（1）（2）中（2）正确；
只有当d=0时，才有Sm，S2m，S3m成等比数列，故（4）正确
故选：D
若也成等比数列，则必须有数列为常数列，与d≠0矛盾，
故（1）（2）中（2）正确；
只有当d=0时，才有Sm，S2m，S3m成等比数列，故（4）正确
故选：D
点评：本题考查等差数列的性质，属基础题．
练习册系列答案
春雨教育同步作文系列答案
相关题目
记等差数列{an}的前n项和为Sn，已知S7=28，S8=36，则S15=（ ）
| A、210 | B、120 |
| C、64 | D、56 |
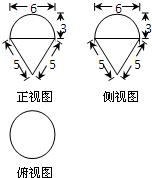一个几何体的三视图如图所示，它的体积为（ ）| A、24π | B、30π |
| C、48π | D、72π |
在△ABC中，AB=1，BC=2，
•
=
，则角B=（ ）
| BA |
| BC |
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
若
=（1，2），
=（-3，m），
⊥
，则m=（ ）
| a |
| b |
| a |
| b |
A、
| ||
B、-
| ||
| C、6 | ||
| D、-6 |