题目内容
已知实数x,y满足x2+y2=2x,则x2y2的取值范围是 .
考点:基本不等式
专题:综合题,不等式的解法及应用
分析:由x2+y2=2x,得y2=2x-x2≥0⇒0≤x≤2,x2y2=2x3-x4,构造函数f(x)=2x3-x4(0≤x≤2),利用导数法可求得函数的单调区间与极值,从而可求其值域.
解答:
解:由x2+y2=2x,得y2=2x-x2≥0,
∴0≤x≤2,x2y2=x2(2x-x2)=2x3-x4.
设f(x)=2x3-x4(0≤x≤2),
则f′(x)=6x2-4x3=2x2(3-2x),
当0<x<
时,f′(x)>0,函数f(x)在(0,
)上单调递增;
当
<x<2时,f′(x)<0,函数f(x)在(
,2)上单调递减,
∴当x=
时,函数取得极大值,也是最大值,f(
)=
,
当x=0、x=2时,f(x)=0,
∴函数f(x)的值域为[0,
],
即0≤x2y2≤
.
故答案为:[0,
].
∴0≤x≤2,x2y2=x2(2x-x2)=2x3-x4.
设f(x)=2x3-x4(0≤x≤2),
则f′(x)=6x2-4x3=2x2(3-2x),
当0<x<
| 3 |
| 2 |
| 3 |
| 2 |
当
| 3 |
| 2 |
| 3 |
| 2 |
∴当x=
| 3 |
| 2 |
| 3 |
| 2 |
| 27 |
| 16 |
当x=0、x=2时,f(x)=0,
∴函数f(x)的值域为[0,
| 27 |
| 16 |
即0≤x2y2≤
| 27 |
| 16 |
故答案为:[0,
| 27 |
| 16 |
点评:本题考查函数的单调性与极值,考查构造函数思想与导数法的应用,着重考查化归思想与创新思维,考查分析问题、解决问题的能力,属于难题.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
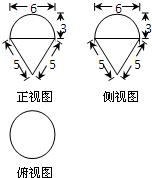 一个几何体的三视图如图所示,它的体积为( )
一个几何体的三视图如图所示,它的体积为( )| A、24π | B、30π |
| C、48π | D、72π |