题目内容
计算:(log23+log43)(log32+log92)= .
考点:对数的运算性质
专题:函数的性质及应用
分析:本题运用对数的运算法则,通过化同底和换底进行化简,得到本题结论.
解答:
解:(log23+log43)(log32+log92)
=(log23+log2
)(log32+log3
)
=log2(3
)log3(2
)
=
log23•
log32
=
.
故答案为:
.
=(log23+log2
| 3 |
| 2 |
=log2(3
| 3 |
| 2 |
=
| 3 |
| 2 |
| 3 |
| 2 |
=
| 9 |
| 4 |
故答案为:
| 9 |
| 4 |
点评:本题考查了对数的运算,用到化同底的化归转化的数学思想,本题难度不大,属于基础题.

练习册系列答案
相关题目
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的部分图象如图示,则下列说法不正确的是( )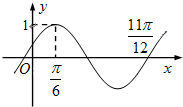
| π |
| 2 |

| A、ω=2 | ||||
B、f(x)的图象关于点(
| ||||
C、k(x)=f(
| ||||
| D、已知函数g(x)=cos(ξx+η)图象与f(x)的对称轴完全相同,则ξ=2 |
把一枚硬币任意抛掷三次,事件A=“至少一次出现反面”,事件B=“恰有一次出现正面”,则P(B|A)=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)在R上满足f(x)=2f(-x)-x2则曲线y=f(x)在点(1,f(1))处的切线方程是( )
| A、y=x |
| B、y=2x-1 |
| C、y=3x-2 |
| D、y=-2x+3 |
函数f(x)=x-
在区间(1,+∞)上是增函数,则实数p的取值范围是( )
| p |
| x |
| A、(-∞,-1] |
| B、(-∞,1] |
| C、[-1,+∞) |
| D、[1,+∞) |
命题p:?x∈R,x3+x-2≥0的否定是( )
| A、?x∈R,x3+x-2<0 |
| B、?x∈R,x3+x-2≥0 |
| C、?x∈R,x3+x-2<0 |
| D、?x∈R,x3+x-2≠0 |