题目内容

把一枚硬币任意抛掷三次，事件A=“至少一次出现反面”，事件B=“恰有一次出现正面”，则P（B|A）=（　　）
A、
1
7
B、
2
7
C、
3
7
D、
4
7
考点：条件概率与独立事件
专题：计算题,概率与统计
分析：由题意，先计算P（AB），P（A），再利用条件概率公式，即可求得结论．
解答： 解：由题意，P（AB）=
3
23
=
3
8
，P（A）=1-
1
23
=
7
8
，
∴P（B|A）=
P(AB)
P(A)
=
3
7
，
故选：C．
点评：本题考查条件概率，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
空间四边形ABCD中，若AB=BC=CD=DA=BD=1，则AC的取值范围是
 
．
若函数f（x）=（k-2）x2+（k-1）x+3是偶函数，则f（x）的递增区间是
 
．
求满足(
1
4
)x-3＞16的x的取值集合是
 
．
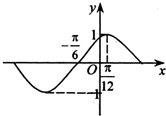函数f（x）=sin（ωx+ϕ）（ω＞0，|ϕ|＜
π
2
）的部分图象如图所示，将y=f（x）的图象向右平移
π
4
个单位后得到函数y=g（x）的图象．则函数y=g（x）的单调增区间为（　　）
A、[kπ-
π
6
，kπ+
π
3
]，k∈Z
B、[kπ+
π
6
，kπ+
π
2
]，k∈Z
C、[kπ-
π
6
，kπ+
2π
3
]，k∈Z
D、[kπ+
π
6
，kπ+
5π
6
]，k∈Z
若x∈（1，10），a=lgx，b=2lgx，c=lg2x，d=lg（lgx），则（　　）
A、a＜b＜c＜d
B、d＜c＜a＜b
C、d＜b＜a＜c
D、b＜d＜c＜a
已知锐角A是△ABC的一个内角，a，b，c是三角形中各角的对应边，若sin2A-cos2A=
1
2
，则b+c与2a的大小关系为
 
．（填＜或＞或≤或≥或=）
计算：（log23+log43）（log32+log92）=
 
．
将二进制数1101化为十进制数为（　　）
A、10B、11C、12D、13

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网