题目内容
已知函数f(x)=lnx+x2-ax,a∈R.
(Ⅰ)当a=3时,求f(x)的单调区间;
(Ⅱ)若x>1,f(x)>0,求a的取值范围.
(Ⅰ)当a=3时,求f(x)的单调区间;
(Ⅱ)若x>1,f(x)>0,求a的取值范围.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:函数的性质及应用
分析:(1)利用导数求函数的单调区间与极值,先求导数,令导数大于0,解得x的范围为函数的增区间,令导数小于0,解得x的范围为函数的减区间.
(2)由f(x)>0,得a<
在x>1时恒成立,令g(x)=
,求g(x)的范围,再约束a的范围.
(2)由f(x)>0,得a<
| lnx+x2 |
| x |
| lnx+x2 |
| x |
解答:
解:(1)解:(1)f(x)的定义域为(0,+∞).
f′(x)=
+2x-3=
,
当0<x<
或x>1时,f′(x)>0,
当
<x<1时,f′(x)<0,
∴f(x)在(0,
)和(1,+∞)上是增函数,在(
,1)上是减函数,
∴(0,
)和(1,+∞)上是增区间,(
,1)上是减区间.
(2)由f(x)>0,得a<
在x>1时恒成立,
令g(x)=
,则g′(x)=
,
令h(x)=1+x2-lnx,则h′(x)=2x-
=
>0,
∴h(x)在(1,+∞)为增函数,h(x)>h(1)=2>0,
∴g′(x)>0,∴g(x)在(1,+∞)为增函数,
∴g(x)>g(1)=1,所以a≤1,即实数a的取值范围为(-∞,1].
f′(x)=
| 1 |
| x |
| 2x2-3x+1 |
| x |
当0<x<
| 1 |
| 2 |
当
| 1 |
| 2 |
∴f(x)在(0,
| 1 |
| 2 |
| 1 |
| 2 |
∴(0,
| 1 |
| 2 |
| 1 |
| 2 |
(2)由f(x)>0,得a<
| lnx+x2 |
| x |
令g(x)=
| lnx+x2 |
| x |
| 1+x2-lnx |
| x2 |
令h(x)=1+x2-lnx,则h′(x)=2x-
| 1 |
| x |
| 2x2-1 |
| x |
∴h(x)在(1,+∞)为增函数,h(x)>h(1)=2>0,
∴g′(x)>0,∴g(x)在(1,+∞)为增函数,
∴g(x)>g(1)=1,所以a≤1,即实数a的取值范围为(-∞,1].
点评:本题主要考查了导数的应用,函数的导数与函数的单调性的关系的应用及恒成立与函数的最值求解的相互转化关系的应用.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
将二进制数1101化为十进制数为( )
| A、10 | B、11 | C、12 | D、13 |
设集合A={1,3,a},B={1,2}且A?B,则a的值为( )
| A、0 | B、1 | C、2 | D、3 |
已知a,b是两条直线,α,β是两个平面,则下列说法中正确的是( )
| A、若a∥b,b∥α,则a∥α |
| B、若a⊥b,b⊥α,则a⊥α |
| C、若α∥β,a?α,则a∥β |
| D、若α⊥β,a?α,则a⊥β |
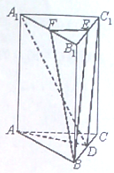 如图,在三棱柱ABC-A1B1C1中,底面为正三角形,AA1⊥平面ABC,D,E,F分别为BC,B1C1,A1B1的中点.
如图,在三棱柱ABC-A1B1C1中,底面为正三角形,AA1⊥平面ABC,D,E,F分别为BC,B1C1,A1B1的中点.