题目内容
函数f（x）在x=x0处导数存在，若p：f′（x0）=0：q：x=x0是f（x）的极值点，则（ ）
| A、p是q的充分必要条件 |
| B、p是q的充分条件，但不是q的必要条件 |
| C、p是q的必要条件，但不是q的充分条件 |
| D、p既不是q的充分条件，也不是q的必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据可导函数的极值和导数之间的关系，利用充分条件和必要条件的定义即可得到结论．
解答：
解：函数f（x）=x3的导数为f'（x）=3x2，由f′（x0）=0，得x0=0，但此时函数f（x）单调递增，无极值，充分性不成立．
根据极值的定义和性质，若x=x0是f（x）的极值点，则f′（x0）=0成立，即必要性成立，
故p是q的必要条件，但不是q的充分条件，
故选：C
根据极值的定义和性质，若x=x0是f（x）的极值点，则f′（x0）=0成立，即必要性成立，
故p是q的必要条件，但不是q的充分条件，
故选：C
点评：本题主要考查充分条件和必要条件的判断，利用函数单调性和极值之间的关系是解决本题的关键，比较基础．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
某几何体的三视图（单位：cm）如图所示，则该几何体的体积是（ ）
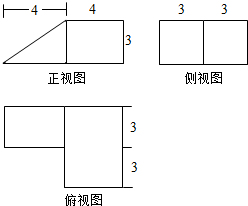
| A、72cm3 |
| B、90cm3 |
| C、108cm3 |
| D、138cm3 |
执行如图所示的程序框图，输出的S值为（ ）
| A、1 | B、3 | C、7 | D、15 |
等差数列{an}的公差为2，若a2，a4，a8成等比数列，则{an}的前n项和Sn=（ ）
| A、n（n+1） | ||
| B、n（n-1） | ||
C、
| ||
D、
|