题目内容
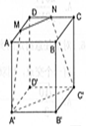 在四棱柱ABCD-A′B′C′D′中,底面ABCD为正方形,侧棱AA′⊥底面A′B′C′D′,AB=2,AA′=4,给出下面五个命题:
在四棱柱ABCD-A′B′C′D′中,底面ABCD为正方形,侧棱AA′⊥底面A′B′C′D′,AB=2,AA′=4,给出下面五个命题:①该四棱柱的外接球的表面积为24π;
②在该四棱柱的12条棱中,与直线B′D异面的棱一共有4条;
③用过点A′、C′的平面去截该四棱柱,且截面为四边形,则截面四边形中至少有一组对边平行;
④用过点A′、C′的平面去截该四棱柱,且截面为梯形,则梯形两腰所在直线的交点一定在直线DD′上;
⑤若截面为四边形A′C′NM,且M、N分别为棱AD、CD的中点,则截面面积为
3
| ||
| 2 |
其中所有是真命题的序号为
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:①根据正四棱柱的对角线即为外接球的直径,再根据球的表面积即可判断;
②由异面直线的定义,列举出与与直线B′D异面的棱,即可判断②;
③运用面面平行的性质定理:如果两个平行平面与第三个平面相交,那么它们的交线相互平行,即可判断;
④可举截面与面AC的交点在AB,CB上,通过延长判断即可得到结论;
⑤首先判断它是等腰梯形,再分别求出底和腰的长,运用梯形面积公式即可得到答案.
②由异面直线的定义,列举出与与直线B′D异面的棱,即可判断②;
③运用面面平行的性质定理:如果两个平行平面与第三个平面相交,那么它们的交线相互平行,即可判断;
④可举截面与面AC的交点在AB,CB上,通过延长判断即可得到结论;
⑤首先判断它是等腰梯形,再分别求出底和腰的长,运用梯形面积公式即可得到答案.
解答:
 解:①由于该四棱柱为正四棱柱,则其外接球的直径2r为正四棱柱的对角线长,
解:①由于该四棱柱为正四棱柱,则其外接球的直径2r为正四棱柱的对角线长,
即2r=
=
,故球的表面积为4πr2=24π,故①正确;
②在该四棱柱的12条棱中,与直线B′D异面的棱有AB,BC,AA',CC',A'D',D'C',
共六条,故②错;
③用过点A′、C′的平面去截该四棱柱,且截面为四边形,则由面A'C'∥面AC,
截面与面AC、A'C'的两条交线平行,则截面四边形中至少有一组对边平行,故③正确;
④用过点A′、C′的平面去截该四棱柱,且截面为梯形,
若截面与面AC的交点在AD,CD上,则梯形两腰所在直线的交点在直线DD'上,
若截面与面AC的交点在AB,CB上,则梯形两腰所在直线的交点在直线BB'上,故④错;
⑤若截面为四边形A′C′NM,且M、N分别为棱AD、CD的中点,则由面面平行的性质定理得,截面为梯形,由正四棱柱得,截面为等腰梯形,且两底MN=
,A'C'=2
,腰长为
,则高为
=
,
故截面面积为
•3
•
=
,故⑤正确.
故答案为:①③⑤.
 解:①由于该四棱柱为正四棱柱,则其外接球的直径2r为正四棱柱的对角线长,
解:①由于该四棱柱为正四棱柱,则其外接球的直径2r为正四棱柱的对角线长,即2r=
| 22+22+42 |
| 24 |
②在该四棱柱的12条棱中,与直线B′D异面的棱有AB,BC,AA',CC',A'D',D'C',
共六条,故②错;
③用过点A′、C′的平面去截该四棱柱,且截面为四边形,则由面A'C'∥面AC,
截面与面AC、A'C'的两条交线平行,则截面四边形中至少有一组对边平行,故③正确;
④用过点A′、C′的平面去截该四棱柱,且截面为梯形,
若截面与面AC的交点在AD,CD上,则梯形两腰所在直线的交点在直线DD'上,
若截面与面AC的交点在AB,CB上,则梯形两腰所在直线的交点在直线BB'上,故④错;
⑤若截面为四边形A′C′NM,且M、N分别为棱AD、CD的中点,则由面面平行的性质定理得,截面为梯形,由正四棱柱得,截面为等腰梯形,且两底MN=
| 2 |
| 2 |
| 17 |
17-
|
| ||
|
故截面面积为
| 1 |
| 2 |
| 2 |
| ||
|
3
| ||
| 2 |
故答案为:①③⑤.
点评:本题以命题的真假判断及应用为载体考查空间直线与平面的位置关系:平行和垂直,同时考查空间两直线的位置关系:异面,考查球内接四棱柱的关系,考查空间想象能力和简单推理能力,以及简单运算能力.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
已知点A(-2,3)在抛物线C:y2=2px的准线上,记C的焦点为F,则直线AF的斜率为( )
A、-
| ||
| B、-1 | ||
C、-
| ||
D、-
|
执行如图所示的程序框图,输出的S值为( )


| A、1 | B、3 | C、7 | D、15 |
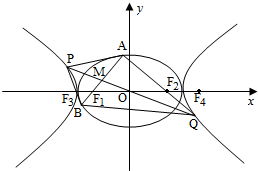 如图,O为坐标原点,椭圆C1:
如图,O为坐标原点,椭圆C1: