题目内容
已知函数f1(x)=
.对于n=1,2,…定义fn+1(x)=f1(fn(x)),若f35(x)=f5(x),f28(x)= .
| 2x-1 |
| x+1 |
考点:数列递推式,数列的函数特性
专题:计算题,函数的性质及应用,等差数列与等比数列
分析:由f35(x)=f5(x)可猜想其具有周期性,再由f1(x)=
,且fn+1(x)=f1(fn(x)),推出f2(x),f3(x),f4(x),f5(x),f6(x),f7(x)从而找到规律,从而求解.
| 2x-1 |
| x+1 |
解答:
解:∵f1(x)=
,且fn+1(x)=f1(fn(x)),
∴f2(x)=
=
;
∴f3(x)=f1(f2(x))=
=
,
∴f4(x)=f1(f3(x))=
=
,
∴f5(x)=f1(f4(x))=
,
∴f6(x)=f1(f5(x))=x,
∴f7(x)=
=f1(x),
∴从f1(x)到f6(x)每6个一循环,
又∵28=4×6+4,
∴f28(x)=f4(x)=
.
故答案为:
.
| 2x-1 |
| x+1 |
∴f2(x)=
2
| ||
|
| x-1 |
| x |
∴f3(x)=f1(f2(x))=
2
| ||
|
| x-2 |
| 2x-1 |
∴f4(x)=f1(f3(x))=
2
| ||
|
| -1 |
| x-1 |
∴f5(x)=f1(f4(x))=
| -x-1 |
| x-2 |
∴f6(x)=f1(f5(x))=x,
∴f7(x)=
| 2x-1 |
| x+1 |
∴从f1(x)到f6(x)每6个一循环,
又∵28=4×6+4,
∴f28(x)=f4(x)=
| -1 |
| x-1 |
故答案为:
| -1 |
| x-1 |
点评:本题考查了数列的函数特性与数列的递推式应用,先猜想,后通过尝试得到周期性,从而求解,属于中档题.

练习册系列答案
相关题目
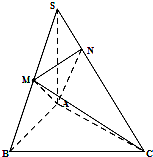 如图,在三棱锥S-ABC中,SA⊥底面ABC,点B为以AC为直径的圆上任意一动点,且SA=AB,点M是SB的中点,AN⊥SC且交SC于点N.
如图,在三棱锥S-ABC中,SA⊥底面ABC,点B为以AC为直径的圆上任意一动点,且SA=AB,点M是SB的中点,AN⊥SC且交SC于点N. 已知椭圆Γ:
已知椭圆Γ: