题目内容

方程x2+（a-2）x+2a-1=0在（0，1）内有且只有一个根，求实数a的范围．
考点：函数零点的判定定理
专题：函数的性质及应用
分析：令f（x）=x2+（a-2）x+2a-1，若函数f（x）在（0，1）内单调，则有f（0）f（1）＜0，由此求得a的范围，．若函数f（x）在（0，1）内不单调，则有
△=(a-2)2-4(2a-1)=0
0＜
2-a
2
＜1
，求得a的值，再把这2个a的范围取并集，即得所求．
解答： 解：∵方程x2+（a-2）x+2a-1=0在（0，1）内有且只有一个根，令f（x）=x2+（a-2）x+2a-1，
若函数f（x）在（0，1）内单调，则有f（0）f（1）＜0，即 （2a-1）（3a-2）＜0，求得
1
2
＜a＜
2
3
．
若函数f（x）在（0，1）内不单调，则有
△=(a-2)2-4(2a-1)=0
0＜
2-a
2
＜1
，求得a=6-2
7
．
综上可得，
1
2
＜a＜
2
3
，或a=6-2
7
．
点评：本题主要考查函数的零点与方程的根的关系，函数零点的判定定理，体现了转化、分类讨论的数学思想，属于基础题．
练习册系列答案
相关题目
已知直线的斜率为4，且在x轴上的截距为2，此直线方程为
 
．
函数f（x）=
x(x+4)，x≥0
x(x-4)，x＜0
，若f（a）＜f（8-a），则a的取值范围是（　　）
A、（-∞，4）
B、（-4，4）
C、（-4，0）
D、（0，4）
已知函数f1（x）=
2x-1
x+1
．对于n=1，2，…定义fn+1（x）=f1（fn（x）），若f35（x）=f5（x），f28（x）=
 
．
三角形三内角的比是7：8：15，则最小内角的弧度数是
 
．
已知
a
=（
3
sin（π+ωx），cosωx），
b
=（sin（
3
2
π-ωx），-cosωx），ω＞0，设f（x）=
a
•
b
的最小正周期为π．
（Ⅰ）求f（x）的单调增区间；
（Ⅱ）当x∈（-
π
3
，
π
6
）时，求f（x）的值域；
（Ⅲ）求满足f（α）=0且-1＜α＜π的角α的值．
已知函数f（x）=
1
2
（sinx+cosx）-
1
2
|sinx-cosx|，x∈[0，2π]，则f（x）的值域是
 
．
已知△ABC的三边长分别为AB=5，BC=4，AC=3，M 是AB边上的点，P是平面ABC外一点．给出下列四个命题：
①若PM丄平面ABC，且M是AB边中点，则有PA=PB=PC；
②若PC=5，PC丄平面ABC，则△PCM面积的最小值为
15
2
；
③若PB=5，PB⊥平面ABC，则三棱锥P-ABC的外接球体积为
125
2
6
π；
④若PC=5，P在平面ABC上的射影是△ABC内切圆的圆心，则三棱锥P-ABC的体积为2
23
；
⑤若PA=5，PA⊥平面ABC，则直线MP与平面PBC所成的最大角正切值为
5
3
．
其中正确命题的序号是
 
． （把你认为正确命题的序号都填上）
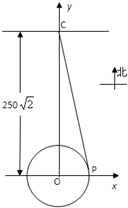某城市交通规划中，拟在以点O为圆心，半径为50m的高架圆形车道外侧P处开一个出口，以与圆形道相切的方式，引申一条直道连接到距圆形道圆心O正北250
2
m的道路上C处（如图），以O为原点，OC为y轴建立如图所示的直角坐标系，求直道PC所在的直线方程，并计算出口P的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网