题目内容
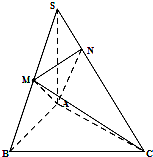 如图,在三棱锥S-ABC中,SA⊥底面ABC,点B为以AC为直径的圆上任意一动点,且SA=AB,点M是SB的中点,AN⊥SC且交SC于点N.
如图,在三棱锥S-ABC中,SA⊥底面ABC,点B为以AC为直径的圆上任意一动点,且SA=AB,点M是SB的中点,AN⊥SC且交SC于点N.(I)求证:SC⊥面AMN
(Ⅱ)当AB=BC时,求二面角N-MA-C的余弦值.
考点:二面角的平面角及求法,直线与平面垂直的判定
专题:空间位置关系与距离,空间角,空间向量及应用
分析:对第(I)问,要证SC⊥面AMN,只需证明SC垂直于平面AMN内的两条相交直线,而已知AN⊥SC,所以只需证明SC⊥AM即可,从而问题转化为证AM⊥平面SBC,由AM⊥SB知,只需证AM⊥BC,转化为证BC⊥平面SAB,即证BC⊥AB,BC⊥SA即可.
对第(Ⅱ)问,利用向量法求解:以A为坐标原点,AB为x轴,过A且与BC平行的直线为y轴,AS为z轴,建立空间直角坐标系A-xyz,分别求出平面AMN与平面AMC的法向量,由两法向量的夹角探求二面角N-MA-C的大小.
对第(Ⅱ)问,利用向量法求解:以A为坐标原点,AB为x轴,过A且与BC平行的直线为y轴,AS为z轴,建立空间直角坐标系A-xyz,分别求出平面AMN与平面AMC的法向量,由两法向量的夹角探求二面角N-MA-C的大小.
解答:
解:(Ⅰ)证明:∵SA⊥底面ABC,BC?底面ABC,∴BC⊥SA.
∵点B在以AC为直径的圆上,则BC⊥AB,∴BC⊥平面SAB,
又∵AM?平面SAB,∴BC⊥AM.
∵SA=AD,M是SD的中点,∴AM⊥SB,∵BC∩SB=B,∴AM⊥平面SBC,
又∵SC?平面SBC,∴AM⊥SC.
由已知AN⊥SC,及AM与AN相交,知SC⊥平面AMN.
(Ⅱ) 如右图所示,以A为坐标原点,AB为x轴,过A且与BC平行的直线为y轴,AS为z轴,建立空间直角坐标系A-xyz,
可设AB=SA=1,则A(0,0,0),B(1,0,0)C(1,1,0),S(0,0,1),M(
,0,
),
∴
=(
,0,
),
=(1,1,0),
=(-1,-1,1).
设平面ACM的法向量为
=(x,y,z),则
,即
,取x=-1,可得一个法向量
=(-1,1,1),
由(Ⅰ)知
为平面AMN的一个法向量,∴cos<
,
>=
=
,
由图易知所求二面角为锐角,故二面角N-MA-C的余弦值是
.
∵点B在以AC为直径的圆上,则BC⊥AB,∴BC⊥平面SAB,
又∵AM?平面SAB,∴BC⊥AM.
∵SA=AD,M是SD的中点,∴AM⊥SB,∵BC∩SB=B,∴AM⊥平面SBC,
又∵SC?平面SBC,∴AM⊥SC.
由已知AN⊥SC,及AM与AN相交,知SC⊥平面AMN.
(Ⅱ) 如右图所示,以A为坐标原点,AB为x轴,过A且与BC平行的直线为y轴,AS为z轴,建立空间直角坐标系A-xyz,

可设AB=SA=1,则A(0,0,0),B(1,0,0)C(1,1,0),S(0,0,1),M(
| 1 |
| 2 |
| 1 |
| 2 |
∴
| AM |
| 1 |
| 2 |
| 1 |
| 2 |
| AC |
| CS |
设平面ACM的法向量为
| n |
|
|
| n |
由(Ⅰ)知
| CS |
| CS |
| n |
| ||||
|
|
| 1 |
| 3 |
由图易知所求二面角为锐角,故二面角N-MA-C的余弦值是
| 1 |
| 3 |
点评:1.本题考查了线面垂直的定义与判定定理,一般情况下,定义用来证明线线垂直,判定定理用来证明线面垂直,应注意体会线线垂直与线面垂直之间的灵活转化.
2.还考查了二面角大小的求法,利用向量法求二面角的大小时,注意两点:
(1)找两半平面的法向量是关键;
(2)常根据原几何体中二面角两半平面的张开程度,或者两法向量在坐标系中的大致指向来确定所求二面角与两半平面法向量夹角的关系.
2.还考查了二面角大小的求法,利用向量法求二面角的大小时,注意两点:
(1)找两半平面的法向量是关键;
(2)常根据原几何体中二面角两半平面的张开程度,或者两法向量在坐标系中的大致指向来确定所求二面角与两半平面法向量夹角的关系.

练习册系列答案
相关题目
函数f(x)=
,若f(a)<f(8-a),则a的取值范围是( )
|
| A、(-∞,4) |
| B、(-4,4) |
| C、(-4,0) |
| D、(0,4) |
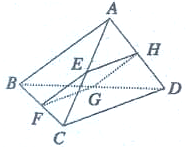 如图四边形EFGH为空间四面体A-BCD的一个截面,若截面为平行四边形.
如图四边形EFGH为空间四面体A-BCD的一个截面,若截面为平行四边形.