题目内容
若函数f（x）=x2+ax+2b在区间（0，1），（1，2）内各有一个零点，则z=
的取值范围是 ．
| 2a+b-4 |
| a |
考点：简单线性规划的应用,函数零点的判定定理
专题：函数的性质及应用
分析：由题意可得
，画出可行域，如图所示，目标函数z=2+
，表示2加上点（a，b）与点M（0，4）连线的斜率．数形结合求得
的范围，可得z的范围．
|
| b-4 |
| a-0 |
| b-4 |
| a-0 |
解答：
解：∵函数f（x）=x2+ax+2b在区间（0，1），（1，2）
内各有一个零点，
∴
，即
，画出可行域，
如图所示：表示△ABC的内部区域，
其中A（-3，1），B（-2，0），C（-1，0）．
目标函数z=2+
，即2加上点（a，b）与点M（0，4）
连线的斜率．
数形结合可得，
的最小值趋于 KAM=
=1，
的最大值趋于 KBM=
=4，
故z的最小值趋于2+1=3，最大值趋于2+4=6，
故答案为（3，6）．
解：∵函数f（x）=x2+ax+2b在区间（0，1），（1，2）内各有一个零点，
∴
|
|
如图所示：表示△ABC的内部区域，
其中A（-3，1），B（-2，0），C（-1，0）．
目标函数z=2+
| b-4 |
| a-0 |
连线的斜率．
数形结合可得，
| b-4 |
| a-0 |
| 4-1 |
| 0+3 |
| b-4 |
| a-0 |
| 4-0 |
| 0+1 |
故z的最小值趋于2+1=3，最大值趋于2+4=6，
故答案为（3，6）．
点评：本题主要考查二次函数的性质，简单的线性规划，斜率公式，体现了转化以及数形结合的数学思想，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
如图，在四棱锥P-ABCD中，侧面PDC是边长为2的正三角形，且与底面垂直，底面ABCD是梯形，AD∥BC且∠ADC=60°，BC=2AD=4．
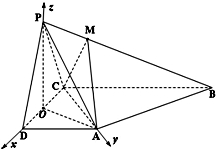
如图，已知四棱锥P-ABCD中，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E、F分别是BC，PC的中点．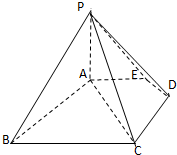
如图，五棱锥P-ABCDE中，PA⊥底面ABCDE，AB∥CD，AC∥ED，AE∥CB，∠ABC=45°，已知锐角A，B满足2tanA=tan（A+B），则tanB的最大值为（ ）
A、2
| ||||
B、
| ||||
C、
| ||||
D、
|