题目内容
已知锐角A,B满足2tanA=tan(A+B),则tanB的最大值为( )
A、2
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:两角和与差的正切函数
专题:三角函数的求值
分析:令tanA=x,tanB=y(x、y>0).则有
=2x,故有 y=
=
,再利用基本不等式求得y的最大值.
| x+y |
| 1-xy |
| x |
| 1+2x2 |
| 1 | ||
|
解答:
解:已知锐角A,B满足2tanA=tan(A+B),为简单起见,
令tanA=x,tanB=y(x、y>0).
则有
=2x,即 y=
=
≤
=
,
当且仅当2x=
时,取等号,故y=tanB的最大值为
,
故选:D.
令tanA=x,tanB=y(x、y>0).
则有
| x+y |
| 1-xy |
| x |
| 1+2x2 |
| 1 | ||
|
| 1 | ||
2
|
| ||
| 4 |
当且仅当2x=
| 1 |
| x |
| ||
| 4 |
故选:D.
点评:本题主要考查两角和的正切公式,基本不等式的应用,属于中档题.

练习册系列答案
相关题目
已知向量
=(1,-2),
=(x,4),且
∥
,则|
-
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
A、5
| ||
B、3
| ||
C、2
| ||
D、2
|
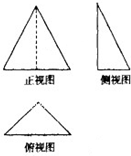 已知一个三棱锥的三视图如图,其中俯视图是斜边长为2的等腰直角三角形,该三棱锥的外接球的半径为
已知一个三棱锥的三视图如图,其中俯视图是斜边长为2的等腰直角三角形,该三棱锥的外接球的半径为| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
某几何体的三视图如图所示,则该几何体的体积为( )


A、
| ||
| B、π | ||
C、
| ||
| D、2π |