题目内容
设F1,F2是双曲线C:
-
=1(b>0)的两个焦点,P是双曲线C上一点,若∠F1PF2=90°且△PF1F2的面积为9,则C的离心率为 .
| x2 |
| 16 |
| y2 |
| b2 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由已知条件,结合双曲线的简单性质求出b2,由此能求出双曲线的离心率.
解答:
解:∵F1,F2是双曲线C:
-
=1(b>0)的两个焦点,
P是双曲线C上一点,∠F1PF2=90°且△PF1F2的面积为9,
∴
,
解得b2=9,
∴a=4,c=
=5,
∴e=
=
.
故答案为:
.
| x2 |
| 16 |
| y2 |
| b2 |
P是双曲线C上一点,∠F1PF2=90°且△PF1F2的面积为9,
∴
|
解得b2=9,
∴a=4,c=
| 16+9 |
∴e=
| c |
| a |
| 5 |
| 4 |
故答案为:
| 5 |
| 4 |
点评:本题考查双曲线的离心率的求法,是中档题,解题时要熟练掌握双曲线的简单性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知向量
=(1,-2),
=(x,4),且
∥
,则|
-
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
A、5
| ||
B、3
| ||
C、2
| ||
D、2
|
 如图,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,且AB=
如图,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,且AB= 如图,圆锥顶点为P,其母线与底面所成的角为60°,AB过底面圆心O点,且∠CBA=60°.
如图,圆锥顶点为P,其母线与底面所成的角为60°,AB过底面圆心O点,且∠CBA=60°. 用红,黄,蓝三种颜色涂标有1,2,…,9的小正方形,如图所示,要求相邻的小正方形的颜色不同,标有3,5,7的颜色相同,问有多少种涂法.
用红,黄,蓝三种颜色涂标有1,2,…,9的小正方形,如图所示,要求相邻的小正方形的颜色不同,标有3,5,7的颜色相同,问有多少种涂法.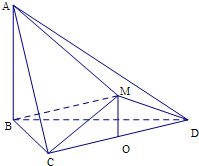 如图,△BCD与△MCD都是边长为2的正三角形,O是CD的中点,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2
如图,△BCD与△MCD都是边长为2的正三角形,O是CD的中点,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2