题目内容
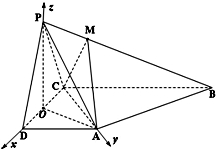 如图,在四棱锥P-ABCD中,侧面PDC是边长为2的正三角形,且与底面垂直,底面ABCD是梯形,AD∥BC且∠ADC=60°,BC=2AD=4.
如图,在四棱锥P-ABCD中,侧面PDC是边长为2的正三角形,且与底面垂直,底面ABCD是梯形,AD∥BC且∠ADC=60°,BC=2AD=4.(1)求证:DC⊥PA;
(2)在PB上是否存在一点M(不包含端点P,B)使得二面角C-AM-B为直二面角,若存在求出PM的长,若不存在请说明理由.
考点:用空间向量求平面间的夹角,与二面角有关的立体几何综合题
专题:空间位置关系与距离,空间向量及应用
分析:(1)取CD的中点O,连结PO,OA,由△PCD为正三角形,推导出△ACD是正三角形,由此能证明AO⊥CD.
(2)以O为坐标原点建立空间直角坐标系,M(a,b,c),
=λ
,求出M(-3λ,2
λ,
-
λ),利用向量法求出λ=
,由此能求出PM的长.
(2)以O为坐标原点建立空间直角坐标系,M(a,b,c),
| PM |
| PB |
| 3 |
| 3 |
| 3 |
| 1 |
| 5 |
解答:
(1)证明:取CD的中点O,连结PO,OA,
∵△PCD为正三角形,
∴PO⊥CD,∵AD=CD=2,
∴△ACD是正三角形,
∴AO⊥CD.
(2)解:∵平面PCD⊥平面ABCD,
平面PCD∩平面ABCD=CD,PO⊥CD,
∴PO⊥平面ABCD,
如图,以O为坐标原点建立空间直角坐标系,
∵侧面PDC是边长为2的正三角形,且与底面垂直,
底面ABCD是梯形,AD∥BC且∠ADC=60°,BC=2AD=4,
∴D(1,0,0),C(-1,0,0),A(0,
,0),
P(0,0,
),B(-3,2
,0),设M(a,b,c),
=λ
,即(a,b,c-
)=λ(-3,2
,-
),
∴a=-3λ,b=2
λ,c=
-
λ,∴M(-3λ,2
λ,
-
λ),
∴
=(-3λ,2
λ-
,
-
λ),
=(-3λ+1,2
λ,
-
λ),
=(-3,
,0),
设平面CAM的法向量
=(x,y,z),
则
•
=0,
•
=0,
∴
,
取z=0,y=
,得x=2-
=-
,
解得λ=
,∴
=(2-
,
,0),
∵设平面ABM的法向量
=(x1,y1,z1),
则
•
=0,
•
=0,
∴
,
∴
=(1,
,
),
∵二面角C-AM-B为直二面角,
∴
•
=2-
+3+0=0,
解得λ=
∵P(0,0,
),B(-3,2
,0),
∴|
|=
|
|=
=
.
∴PM的长为
.
∵△PCD为正三角形,
∴PO⊥CD,∵AD=CD=2,
∴△ACD是正三角形,

∴AO⊥CD.
(2)解:∵平面PCD⊥平面ABCD,
平面PCD∩平面ABCD=CD,PO⊥CD,
∴PO⊥平面ABCD,
如图,以O为坐标原点建立空间直角坐标系,
∵侧面PDC是边长为2的正三角形,且与底面垂直,
底面ABCD是梯形,AD∥BC且∠ADC=60°,BC=2AD=4,
∴D(1,0,0),C(-1,0,0),A(0,
| 3 |
P(0,0,
| 3 |
| 3 |
| PM |
| PB |
| 3 |
| 3 |
| 3 |
∴a=-3λ,b=2
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
∴
| AM |
| 3 |
| 3 |
| 3 |
| 3 |
| CM |
| 3 |
| 3 |
| 3 |
| AB |
| 3 |
设平面CAM的法向量
| m |
则
| m |
| AM |
| m |
| CM |
∴
|
取z=0,y=
| 3 |
| 1 |
| λ |
| 6λ |
| -3λ+1 |
解得λ=
| 1 |
| 5 |
| m |
| 1 |
| λ |
| 3 |
∵设平面ABM的法向量
| n |
则
| n |
| AM |
| n |
| AB |
∴
|
∴
| n |
| 3 |
| ||||
| 1-λ |
∵二面角C-AM-B为直二面角,
∴
| m |
| n |
| 1 |
| λ |
解得λ=
| 1 |
| 5 |
∵P(0,0,
| 3 |
| 3 |
∴|
| PM |
| 1 |
| 5 |
| PB |
| 1 |
| 5 |
| 9+12+3 |
2
| ||
| 5 |
∴PM的长为
2
| ||
| 5 |
点评:本题考查异面直线垂直的证明,考查线段长的求法,综合性强,难度较大,解题时要注意向量法的合理运用.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 如图,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,且AB=
如图,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,且AB= 如图,在四棱锥A-BCDE中,底面四边形BCDE是等腰梯形,BC∥DE,∠DCB=45°,O是BC的中点,AO=
如图,在四棱锥A-BCDE中,底面四边形BCDE是等腰梯形,BC∥DE,∠DCB=45°,O是BC的中点,AO= 某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点.不包括右端点.如第一组表示收入在[1000,1500)
某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点.不包括右端点.如第一组表示收入在[1000,1500)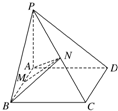 如图所示,已知PA⊥矩形ABCD所在平面,M,N分别是AB,PC的中点.
如图所示,已知PA⊥矩形ABCD所在平面,M,N分别是AB,PC的中点.