题目内容
 如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC,PC的中点.
如图,已知四棱锥P-ABCD中,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC,PC的中点.(1)证明:AE⊥平面PAD;
(2)若H为PD上的动点,EH与平面PAD所成最大角的正切值为
| 3 |
考点:与二面角有关的立体几何综合题,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)通过证明AE⊥BC.PA⊥AE.说明PA?平面PAD,AD?平面PAD且PA∩AD=A,利用直线与平面垂直的判定定理证明AE⊥平面PAD.
(2)解:设AB=2,H为PD上任意一点,连结AH,EH.由(1)知AE⊥平面PAD,则∠EHA为EH与平面PAD所成的角.(法一)在Rt△ESO中,求出cos∠ESO的值即可.
(法二)由(1)知AE,AD,AP两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系,求出平面AEF的一个法向量为
,求出平面AFC的一个法向量
,利用二面角公式求出二面角E-AF-C的余弦值.
(2)解:设AB=2,H为PD上任意一点,连结AH,EH.由(1)知AE⊥平面PAD,则∠EHA为EH与平面PAD所成的角.(法一)在Rt△ESO中,求出cos∠ESO的值即可.
(法二)由(1)知AE,AD,AP两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系,求出平面AEF的一个法向量为
| m |
| BD |
解答:
 (1)证明:由四边形ABCD为菱形,∠ABC=60°,可得△ABC为正三角形.
(1)证明:由四边形ABCD为菱形,∠ABC=60°,可得△ABC为正三角形.
∵E为BC的中点,∴AE⊥BC.
又BC∥AD,因此AE⊥AD.
∵PA⊥平面ABCD,AE?平面ABCD,∴PA⊥AE.
而PA?平面PAD,AD?平面PAD且PA∩AD=A,
∴AE⊥平面PAD.(4分)
(2)解:设AB=2,H为PD上任意一点,连结AH,EH.
由(1)知AE⊥平面PAD,则∠EHA为EH与平面PAD所成的角.
在Rt△EAH中,AE=
,∴当AH最短时,∠EHA最大,
即当AH⊥PD时,∠EHA最大.此时tan∠EHA=
=
=
,
因此AH=1.又AD=2,∴∠ADH=30°,∴PA=AD tan 30°=
.(8分)
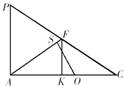
(法一)∵PA⊥平面ABCD,PA?平面PAC,∴平面PAC⊥平面ABCD.
过E作EO⊥AC于O,则EO⊥平面PAC,
过O作OS⊥AF于S,连结ES,则∠ESO为二面角E-AF-C的平面角,
在Rt△AOE中,EO=AE•sin 30°=
,AO=AE•cos 30°=
.
又F是PC的中点,如图,PC=
=
,
∴AF=
PC=
,sin∠SAO=
=
,
在Rt△ASO中,SO=AO•sin∠SAO=
,
∴SE=
=
=
,
在Rt△ESO中,cos∠ESO=
=
=
,
即所求二面角的余弦值为
.(12分)
(法二)由(1)知AE,AD,AP两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系,又E,F分别为BC,PC的中点,∴A(0,0,0),B(
,-1,0),C(
,1,0),D(0,2,0),P(0,0,2),E(
,0,0),F(
,
,
),
∴
=(
,0,0),
=(
,
,
).
设平面AEF的一个法向量为
=(x1,y1,z1),
则
因此
,
取z1=-1,则m=(0,
,-1),
∵BD⊥AC,BD⊥PA,PA∩AC=A,
∴BD⊥平面AFC,故
为平面AFC的一个法向量.
又
=(-
,3,0),
∴cos<
,
>=
=
=
.
∵二面角E-AF-C为锐角,
∴所求二面角的余弦值为
.(12分)
 (1)证明:由四边形ABCD为菱形,∠ABC=60°,可得△ABC为正三角形.
(1)证明:由四边形ABCD为菱形,∠ABC=60°,可得△ABC为正三角形.∵E为BC的中点,∴AE⊥BC.
又BC∥AD,因此AE⊥AD.
∵PA⊥平面ABCD,AE?平面ABCD,∴PA⊥AE.
而PA?平面PAD,AD?平面PAD且PA∩AD=A,
∴AE⊥平面PAD.(4分)
(2)解:设AB=2,H为PD上任意一点,连结AH,EH.
由(1)知AE⊥平面PAD,则∠EHA为EH与平面PAD所成的角.
在Rt△EAH中,AE=
| 3 |
即当AH⊥PD时,∠EHA最大.此时tan∠EHA=
| AE |
| AH |
| ||
| AH |
| 3 |
因此AH=1.又AD=2,∴∠ADH=30°,∴PA=AD tan 30°=
2
| ||
| 3 |
(法一)∵PA⊥平面ABCD,PA?平面PAC,∴平面PAC⊥平面ABCD.
过E作EO⊥AC于O,则EO⊥平面PAC,
过O作OS⊥AF于S,连结ES,则∠ESO为二面角E-AF-C的平面角,
在Rt△AOE中,EO=AE•sin 30°=
| ||
| 2 |
| 3 |
| 2 |
又F是PC的中点,如图,PC=
| PA2+AC2 |
4
| ||
| 3 |
∴AF=
| 1 |
| 2 |
2
| ||
| 3 |
| FK |
| AF |
| 1 |
| 2 |

在Rt△ASO中,SO=AO•sin∠SAO=
| 3 |
| 4 |
∴SE=
| EO2+SO2 |
4+
|
| ||
| 4 |
在Rt△ESO中,cos∠ESO=
| SO |
| SE |
| ||||
|
| ||
| 7 |
即所求二面角的余弦值为
| ||
| 7 |
(法二)由(1)知AE,AD,AP两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系,又E,F分别为BC,PC的中点,∴A(0,0,0),B(
| 3 |
| 3 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 3 |
∴
| AE |
| 3 |
| AF |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 3 |

设平面AEF的一个法向量为
| m |
则
|
|
取z1=-1,则m=(0,
2
| ||
| 3 |
∵BD⊥AC,BD⊥PA,PA∩AC=A,
∴BD⊥平面AFC,故
| BD |
又
| BD |
| 3 |
∴cos<
| m |
| BD |
| ||||
|
|
2
| |||||||
|
| ||
| 7 |
∵二面角E-AF-C为锐角,
∴所求二面角的余弦值为
| ||
| 7 |
点评:本题考查直线与平面垂直的判定定理,二面角的求法,解决此类问题的关键是熟练掌握几何体的结构特征,以便利用已知条件得到空间的线面关系,并且便于建立坐标系利用向量的有关运算解决空间角等问题.

练习册系列答案
相关题目
 某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点.不包括右端点.如第一组表示收入在[1000,1500)
某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点.不包括右端点.如第一组表示收入在[1000,1500)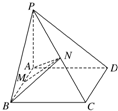 如图所示,已知PA⊥矩形ABCD所在平面,M,N分别是AB,PC的中点.
如图所示,已知PA⊥矩形ABCD所在平面,M,N分别是AB,PC的中点. 如图,圆锥顶点为P,其母线与底面所成的角为60°,AB过底面圆心O点,且∠CBA=60°.
如图,圆锥顶点为P,其母线与底面所成的角为60°,AB过底面圆心O点,且∠CBA=60°.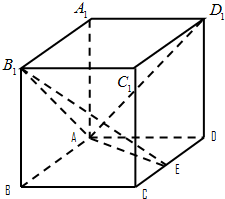 如图,在长方体ABCD-A1B1C1D1中AA1=AD=1,E为CD中点.
如图,在长方体ABCD-A1B1C1D1中AA1=AD=1,E为CD中点. 用红,黄,蓝三种颜色涂标有1,2,…,9的小正方形,如图所示,要求相邻的小正方形的颜色不同,标有3,5,7的颜色相同,问有多少种涂法.
用红,黄,蓝三种颜色涂标有1,2,…,9的小正方形,如图所示,要求相邻的小正方形的颜色不同,标有3,5,7的颜色相同,问有多少种涂法.