题目内容
过双曲线
-
=1(a>0,b>0)的左焦点F(-c,0)(c>0),作倾斜角为
的直线FE交该双曲线右支于点P,若
=
(
+
),且
•
=0,则双曲线的离心率为 .
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 6 |
| OE |
| 1 |
| 2 |
| OF |
| OP |
| OE |
| EF |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由题设条件结合双曲线的性质,推导出OE=
a,EF=
a,OE⊥EF,OF=c,由此利用勾股定理能求出a,c间的等量关系,从而能求出双曲线的离心率.
| 1 | ||
|
| ||
|
解答:
解: 如图,设双曲线的右焦点为Q,FQ的中点为O,连结OE,PQ,
如图,设双曲线的右焦点为Q,FQ的中点为O,连结OE,PQ,
∵
=
(
+
),且
•
=0,
∴OE
PQ,OE⊥EF,
又∵PF-PQ=2a,∴EF-OE=a,
∵直线FE的倾斜角为
,
∴
=
,
∴EF=
OE,
∴
OE-OE=(
-1)OE=a,
∴OE=
a,EF=
a,
∵OE⊥EF,OF=c,
∴(
a)2+(
a)2=c2,
解得c=
a=(
+1)a,
∴e=
=
+1.
故答案为:
+1.
 如图,设双曲线的右焦点为Q,FQ的中点为O,连结OE,PQ,
如图,设双曲线的右焦点为Q,FQ的中点为O,连结OE,PQ,∵
| OE |
| 1 |
| 2 |
| OF |
| OP |
| OE |
| EF |
∴OE
| ∥ |
. |
| 1 |
| 2 |
又∵PF-PQ=2a,∴EF-OE=a,
∵直线FE的倾斜角为
| π |
| 6 |
∴
| OE |
| EF |
| 1 | ||
|
∴EF=
| 3 |
∴
| 3 |
| 3 |
∴OE=
| 1 | ||
|
| ||
|
∵OE⊥EF,OF=c,
∴(
| 1 | ||
|
| ||
|
解得c=
|
| 3 |
∴e=
| c |
| a |
| 3 |
故答案为:
| 3 |
点评:本题考查双曲线的离心率的求法,是中档题,解题时要认真审题,注意数形结合思想的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点.不包括右端点.如第一组表示收入在[1000,1500)
某市统计局就某地居民的月收入调查了10000人,并根据所得数据画出样本的频率分布直方图(每个分组包括左端点.不包括右端点.如第一组表示收入在[1000,1500) 用红,黄,蓝三种颜色涂标有1,2,…,9的小正方形,如图所示,要求相邻的小正方形的颜色不同,标有3,5,7的颜色相同,问有多少种涂法.
用红,黄,蓝三种颜色涂标有1,2,…,9的小正方形,如图所示,要求相邻的小正方形的颜色不同,标有3,5,7的颜色相同,问有多少种涂法.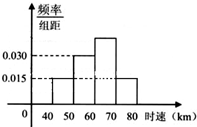 已知200辆汽车在通过某一段公路的时速的频率分布直方图如图所示,则时速在[60,70]之间的汽车大约有
已知200辆汽车在通过某一段公路的时速的频率分布直方图如图所示,则时速在[60,70]之间的汽车大约有