题目内容
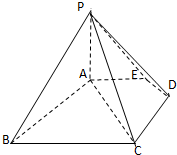 如图,五棱锥P-ABCDE中,PA⊥底面ABCDE,AB∥CD,AC∥ED,AE∥CB,∠ABC=45°,AB=PA=2
如图,五棱锥P-ABCDE中,PA⊥底面ABCDE,AB∥CD,AC∥ED,AE∥CB,∠ABC=45°,AB=PA=2| 2 |
(1)求点B到平面PCD的距离;
(2)求二面角P-BC-A的正弦值;
(3)在棱PA上是否存在一点M,使得DM∥面PBC,若存在,求出DM的长,若不存在,说明理由.
考点:与二面角有关的立体几何综合题,点、线、面间的距离计算
专题:空间位置关系与距离
分析:(1)以A为坐标原点,AB、AC、AP所在直线为x轴、y轴、z轴,建立坐标系,利用向量法能求出点B到平面PCD的距离.
(2)分别求出平面PBC的法向量的面ABC的一个法向量,利用向量法能求出二面角P-BC-A的余弦值,再由三角函数知识能求出其正弦值.
(3)假设存在这样的点M(0,0,z),再由向量法进行计算.
(2)分别求出平面PBC的法向量的面ABC的一个法向量,利用向量法能求出二面角P-BC-A的余弦值,再由三角函数知识能求出其正弦值.
(3)假设存在这样的点M(0,0,z),再由向量法进行计算.
解答:
(本小题满分14分)
解:(1)∵∠ABC=45°,AB=PA=2
,BC=2AE=4,
∴AC=
=
=2
,
∴AB⊥AC,
以A为坐标原点,AB、AC、AP所在直线为x轴、y轴、z轴,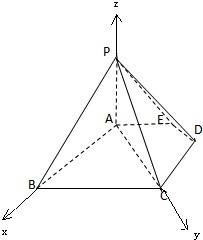
建立坐标系如图,
则由题意知:A(0,0,0),P(0,0,2
),B(2
,0,0),
C(0,2
,0),D(-
,2
,0),
设平面PCD的法向量为
=(x,y,1),
则
,
∴
=(0,1,1).
又
=(-2
,2
,0),
∴点B到平面PCD的距离为d=
=2
(2)设平面PBC的法向量为
=(x,y,1),
∵
=(2
,0,-2
),
=(-2
,2
,0),
∴
,
∴
=(1,1,1),
∵面ABC的一个法向量为
=(0,0,1).
∴cosθ=
=
,
∴sinθ=
∴二面角P-BC-A的正弦值为
.
(3)假设存在这样的点M(0,0,z),(0≤z≤2
),
则
=(
,-2
,z).
由(2)得,面PBC的一个法向量为
=(1,1,1),
当DM∥面PBC时,
•
=
-2
+z=0.
解得z=
,故存在点M(0,0,
),
且DM=
=2
.
解:(1)∵∠ABC=45°,AB=PA=2
| 2 |
∴AC=
| AB2+BC2-2AB•BC•cos45° |
8+16-2×2
|
| 2 |
∴AB⊥AC,
以A为坐标原点,AB、AC、AP所在直线为x轴、y轴、z轴,

建立坐标系如图,
则由题意知:A(0,0,0),P(0,0,2
| 2 |
| 2 |
C(0,2
| 2 |
| 2 |
| 2 |
设平面PCD的法向量为
| n |
则
|
∴
| n |
又
| BC |
| 2 |
| 2 |
∴点B到平面PCD的距离为d=
|
| ||||
|
|
(2)设平面PBC的法向量为
| m1 |
∵
| PB |
| 2 |
| 2 |
| BC |
| 2 |
| 2 |
∴
|
∴
| m1 |
∵面ABC的一个法向量为
| m2 |
∴cosθ=
|
| ||||
|
|
| ||
| 3 |
∴sinθ=
| ||
| 3 |
∴二面角P-BC-A的正弦值为
| ||
| 3 |
(3)假设存在这样的点M(0,0,z),(0≤z≤2
| 2 |
则
| DM |
| 2 |
| 2 |
由(2)得,面PBC的一个法向量为
| m |
当DM∥面PBC时,
| DM |
| m |
| 2 |
| 2 |
解得z=
| 2 |
| 2 |
且DM=
| 2+8+2 |
| 3 |
点评:本题考查点到平面的距离的求法,考查二面角的正弦值的求法,考查满足条件的点的求法,解题时要注意向量法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图所示,已知PA⊥矩形ABCD所在平面,M,N分别是AB,PC的中点.
如图所示,已知PA⊥矩形ABCD所在平面,M,N分别是AB,PC的中点. 如图,在长方体ABCD-A1B1C1D1中AA1=AD=1,E为CD中点.
如图,在长方体ABCD-A1B1C1D1中AA1=AD=1,E为CD中点. 用红,黄,蓝三种颜色涂标有1,2,…,9的小正方形,如图所示,要求相邻的小正方形的颜色不同,标有3,5,7的颜色相同,问有多少种涂法.
用红,黄,蓝三种颜色涂标有1,2,…,9的小正方形,如图所示,要求相邻的小正方形的颜色不同,标有3,5,7的颜色相同,问有多少种涂法. 如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点.
如图,四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PB⊥BC,PD⊥CD,且PA=2,E为PD中点.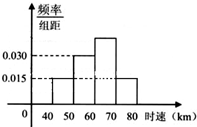 已知200辆汽车在通过某一段公路的时速的频率分布直方图如图所示,则时速在[60,70]之间的汽车大约有
已知200辆汽车在通过某一段公路的时速的频率分布直方图如图所示,则时速在[60,70]之间的汽车大约有