题目内容
已知实数x,y满足
,则z=x+2y的最大值是 .
|
考点:简单线性规划
专题:计算题,作图题,不等式的解法及应用
分析:由题意作出其平面区域,将z=x+2y化为y=-
x+
z,
z相当于直线y=-
x+
z的纵截距,由几何意义可得.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:由题意作出其平面区域,

将z=x+2y化为y=-
x+
z,
z相当于直线y=-
x+
z的纵截距,由几何意义可得,
过点A时有最大值,
解得,A(
,
),
则z=x+2y的最大值是:
+2×
=
,
故答案为:
.

将z=x+2y化为y=-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
过点A时有最大值,
|
| 1 |
| 2 |
| 3 |
| 2 |
则z=x+2y的最大值是:
| 1 |
| 2 |
| 3 |
| 2 |
| 7 |
| 2 |
故答案为:
| 7 |
| 2 |
点评:本题考查了简单线性规划,作图要细致认真,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
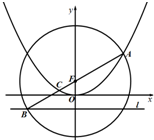 如图,已知点F是抛物线x2=4y的焦点,直线l为准线,点A是抛物线上一点.以F点为圆心,|AF|为半径作圆M交抛物线的准线l于点B.若A,B,F三点共线,则|AC|=( )
如图,已知点F是抛物线x2=4y的焦点,直线l为准线,点A是抛物线上一点.以F点为圆心,|AF|为半径作圆M交抛物线的准线l于点B.若A,B,F三点共线,则|AC|=( )