题目内容
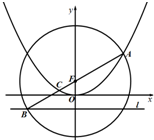如图，已知点F是抛物线x2=4y的焦点，直线l为准线，点A是抛物线上一点．以F点为圆心，|AF|为半径作圆M交抛物线的准线l于点B．若A，B，F三点共线，则|AC|=（ ）A、
| ||
| B、16 | ||
C、
| ||
| D、8 |
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：由题意A、B、F三点在同一条直线上，由直径所对的圆周角为直角，可得∠ADB=90°．利用抛物线的定义可得到∠ABD=30°．即可得到直线的斜率，得到直线的方程，代入抛物线方程，利用弦长公式，即可得出结论．
解答：
解：以F点为圆心，|AF|为半径作圆M交抛物线的准线l于点B，D，则
由题意A、B、F三点在同一条直线m上，
∴∠ADB=90°．
∴∠ABD=30°．
∴直线AB的斜率为
．
∴直线AB的方程为y=
x+1．
代入x2=4y，可得x2-
x-4=0，
∴|AC|=
•
=
，
故选：A．
由题意A、B、F三点在同一条直线m上，
∴∠ADB=90°．
∴∠ABD=30°．
∴直线AB的斜率为
| ||
| 3 |
∴直线AB的方程为y=
| ||
| 3 |
代入x2=4y，可得x2-
4
| ||
| 3 |
∴|AC|=
1+
|
(
|
| 16 |
| 3 |
故选：A．
点评：本题考查了抛物线的定义标准方程及其性质、圆的性质、含30°的直角三角形的性质、直线的方程等基础知识与基本技能方法，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知命题p：?x∈R，使sinx=
；命题q：?x∈R，都有x2+x+1＞0．给出下列结论：
①命题“p∧q”是真命题；
②命题“￢p∨q”是假命题
③命题“￢p∨q”是真命题；
④命题“p∨￢q”是假命题；
其中正确的是（ ）
| ||
| 2 |
①命题“p∧q”是真命题；
②命题“￢p∨q”是假命题
③命题“￢p∨q”是真命题；
④命题“p∨￢q”是假命题；
其中正确的是（ ）
| A、②③ | B、②④ | C、③④ | D、①②③ |
命题“若一个数是负数，则它的平方是正数”的逆否命题是（ ）
| A、“若一个数是负数，则它的平方不是正数” |
| B、“若一个数的平方是正数，则它是负数” |
| C、“若一个数不是负数，则它的平方不是正数” |
| D、“若一个数的平方不是正数，则它不是负数” |
定义在R上的奇函数f（x）满足：x≤0时，f（x）=ax+b（a＞0且a≠1），f（1）=
，则f（2）=（ ）
| 1 |
| 2 |
A、-
| ||
B、
| ||
| C、3 | ||
| D、-3 |
若集合A={0，1，2，3}，B={1，2，4}，则集合A∩B=（ ）
| A、{0，1，2，3，4} |
| B、{1，2，3，4} |
| C、{1，2} |
| D、{0} |