题目内容
已知等差数列前三项为a,4,3a,前n项的和为Sn,Sk=2550.
(1)求a及k的值;
(2)求证
+
+…+
<1.
(1)求a及k的值;
(2)求证
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
考点:数列与不等式的综合
专题:等差数列与等比数列,不等式的解法及应用
分析:(1)直接由等差数列的性质结合给出的前三项列式求得a的值,则公差可求,代入等差数列的前k项和得答案;
(2)直接利用裂项相消法求
+
+…+
的和,然后放缩证得数列不等式.
(2)直接利用裂项相消法求
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
解答:
(1)解:设该等差数列为{an},
则a1=a,a2=4,a3=3a,
由已知有a+3a=2×4,解得a1=a=2,公差d=a2-a1=2,
将Sk=2550代入公式Sk=ka1+
d,得k=50,k=-51(舍去)
∴a=2,k=50;
(2)证明:由 Sn=na1+
d,
得 Sn=n(n+1),
=
=
-
,
+
+…+
=
+
+…+
=(1-
)+(
-
)+…+(
-
)
=1-
<1.
则a1=a,a2=4,a3=3a,
由已知有a+3a=2×4,解得a1=a=2,公差d=a2-a1=2,
将Sk=2550代入公式Sk=ka1+
| k(k-1) |
| 2 |
∴a=2,k=50;
(2)证明:由 Sn=na1+
| n(n-1) |
| 2 |
得 Sn=n(n+1),
| 1 |
| Sn |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
=
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| n(n+1) |
=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=1-
| 1 |
| n+1 |
点评:本题考查了数列的通项公式,考查了等差数列的前n项和,考查了裂项相消法求数列的和,训练了放缩法证明数列不等式,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
直线y=
的倾斜角为( )
| π |
| 4 |
| A、0 | ||
B、
| ||
C、
| ||
| D、不存在 |
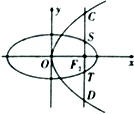 如图,椭圆E:
如图,椭圆E: