题目内容
已知等比数列{an}满足2a1+a3=3a2,且a3+2是a2,a4的等差中项,n∈N*.
(1)求数列{an}的通项公式;
(2)若bn=an+log2an,Sn为数列{bn}的前n项和,求使Sn-2n+1-8≤0成立的n的取值集合.
(1)求数列{an}的通项公式;
(2)若bn=an+log2an,Sn为数列{bn}的前n项和,求使Sn-2n+1-8≤0成立的n的取值集合.
考点:数列的求和,等比数列的通项公式
专题:综合题
分析:(1)利用等比数列{an}满足2a1+a3=3a2,且a3+2是a2,a4的等差中项,建立方程,求出q,a1,即可求数列{an}的通项公式;
(2)利用分组求和,再解不等式,即可得出结论.
(2)利用分组求和,再解不等式,即可得出结论.
解答:
解:(1)∵a3+2是a2和a4的等差中项,∴2(a3+2)=a2+a4
∵2a1+a3=3a2,∴q=2(q=1舍去),a1=2
∴an=a1qn-1=2n….(6分)
(2)bn=an+log2an=2n+n.…(7分)
所以Sn=(2+4+…+2n)+(1+2+…+n)=
+
=2n+1-2+
n+
n2 ….(10分)
因为Sn-2n+1-8≤0,所以n2+n-20≤0
解得-5≤n≤4,故所求的n的取值集合为{1,2,3,4}….(12分)
∵2a1+a3=3a2,∴q=2(q=1舍去),a1=2
∴an=a1qn-1=2n….(6分)
(2)bn=an+log2an=2n+n.…(7分)
所以Sn=(2+4+…+2n)+(1+2+…+n)=
| 2(1-2n) |
| 1-2 |
| n(1+n) |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
因为Sn-2n+1-8≤0,所以n2+n-20≤0
解得-5≤n≤4,故所求的n的取值集合为{1,2,3,4}….(12分)
点评:本题考查等比数列求通项公式和等差、等比中项的概念,等差数列和等比数列之间的相互转化,考查运算能力,属中档题.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
直线y=
的倾斜角为( )
| π |
| 4 |
| A、0 | ||
B、
| ||
C、
| ||
| D、不存在 |
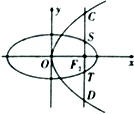 如图,椭圆E:
如图,椭圆E: