题目内容
设D,E分别是△ABC的边AB,BC上的点,AD=
AB,BE=
BC,若
=λ1
+λ2
(λ1,λ2为实数),则λ1+λ2的值为( )
| 1 |
| 2 |
| 2 |
| 3 |
| DE |
| AB |
| AC |
| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
考点:平面向量的基本定理及其意义
专题:计算题,平面向量及应用
分析:作出图形,根据向量的线性运算规则,得
=
-
=
-
=
(
-
)-
=
-
,再由分解的唯一性得出λ1与λ2的值即可.
| DE |
| BE |
| BD |
| 2 |
| 3 |
| BC |
| 1 |
| 2 |
| BA |
| 2 |
| 3 |
| AC |
| AB |
| 1 |
| 2 |
| BA |
| 2 |
| 3 |
| AC |
| 1 |
| 6 |
| AB |
解答:
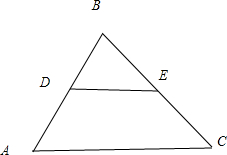 解:由题意,如图,
解:由题意,如图,
因为AD=
AB,BE=
BC,
∴
=
-
=
-
=
(
-
)-
=
-
,
又
=λ1
+λ2
(λ1,λ2为实数),
∴λ1=-
,λ2=
,
∴λ1+λ2=-
+
=
.
故选C.
 解:由题意,如图,
解:由题意,如图,因为AD=
| 1 |
| 2 |
| 2 |
| 3 |
∴
| DE |
| BE |
| BD |
| 2 |
| 3 |
| BC |
| 1 |
| 2 |
| BA |
| 2 |
| 3 |
| AC |
| AB |
| 1 |
| 2 |
| BA |
| 2 |
| 3 |
| AC |
| 1 |
| 6 |
| AB |
又
| DE |
| AB |
| AC |
∴λ1=-
| 1 |
| 6 |
| 2 |
| 3 |
∴λ1+λ2=-
| 1 |
| 6 |
| 2 |
| 3 |
| 1 |
| 2 |
故选C.
点评:本题考查向量基本定理,分解的唯一性是此类求参数题建立方程依据,注意体会这一规律.

练习册系列答案
相关题目
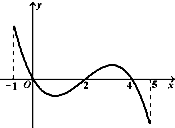 已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.下列关于f(x)的命题:
已知函数f(x)的定义域为[-1,5],部分对应值如下表,f(x)的导函数y=f′(x)的图象如图所示.下列关于f(x)的命题: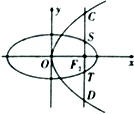 如图,椭圆E:
如图,椭圆E: