题目内容
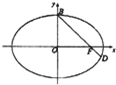 如图,已知F是椭圆C的一个焦点,B是短轴的一个端点,线段BF的延长线交椭圆C于点D,且
如图,已知F是椭圆C的一个焦点,B是短轴的一个端点,线段BF的延长线交椭圆C于点D,且| BF |
| FD |
考点:椭圆的简单性质
专题:平面向量及应用,圆锥曲线的定义、性质与方程
分析:由椭圆的性质求出|BF|的值,利用已知的向量间的关系、三角形相似求出D的横坐标,再由椭圆的第二定义求出|
|的值,又由
=3
建立关于a、c的方程,解方程求出
的值.
| FD |
| BF |
| FD |
| c |
| a |
解答:
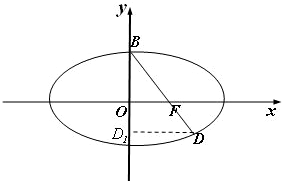 解:如图,BF=
解:如图,BF=
=a,
作DD1⊥y轴于点D1,则由
=3
得:
=
=
,
所以,|
|=
|
|=
c,
即xD=
c,
由椭圆的第二定义得|
|=e(
-
c)=a-
,
又由|
|=3|
|,得a=3(a-
),a2=2c2,解得e=
=
,
故答案为:
 解:如图,BF=
解:如图,BF=| b2+c2 |
作DD1⊥y轴于点D1,则由
| BF |
| FD |
|
| ||
|
|
|
| ||
|
|
| 3 |
| 4 |
所以,|
| DD1 |
| 4 |
| 3 |
| OF |
| 4 |
| 3 |
即xD=
| 4 |
| 3 |
由椭圆的第二定义得|
| FD |
| a2 |
| c |
| 4 |
| 3 |
| 4c2 |
| 3a |
又由|
| BF |
| FD |
| 4c2 |
| 3a |
| c |
| a |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本小题主要考查椭圆的方程与几何性质、第二定义、平面向量知识,考查了数形结合思想、方程思想,本题凸显解析几何的特点:“数研究形,形助数”,利用几何性质可寻求到简化问题的捷径.

练习册系列答案
相关题目
直线y=
的倾斜角为( )
| π |
| 4 |
| A、0 | ||
B、
| ||
C、
| ||
| D、不存在 |
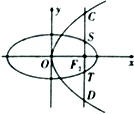 如图,椭圆E:
如图,椭圆E: