题目内容
根据下列条件解三角形:c=
,A=45°,a=2.
| 6 |
考点:解三角形
专题:计算题,解三角形
分析:根据正弦定理,结合三角形的边角关系即可求出三角形的内角和边长.
解答:
解:∵
=
,∴sinC=
=
=
,
∴C=60°或120°,
当C=60°时,B=180°-A-C=75°,b=
=
=
+1;
当C=120°时,B=180°-A-C=15°,b=
=
=
-1.
故b=
+1,C=60°,B=75°,或b=
-1,C=120°,B=15°.
| a |
| sinA |
| c |
| sinC |
| csinA |
| a |
| ||||||
| 2 |
| ||
| 2 |
∴C=60°或120°,
当C=60°时,B=180°-A-C=75°,b=
| csinB |
| sinC |
| ||||||||
|
| 3 |
当C=120°时,B=180°-A-C=15°,b=
| csinB |
| sinC |
| ||||||||
|
| 3 |
故b=
| 3 |
| 3 |
点评:本题主要考查正弦定理的应用,利用正弦定理是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
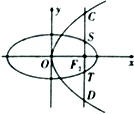 如图,椭圆E:
如图,椭圆E: