题目内容
已知实数x,y满足
,则目标函数z=x2+y2的最小值为 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:本题考察简单的线性规划问题,先由不等式组画出可行域,再将目标函数中z转化为距离处理.
解答:
 解:不等式组表示的平面区域如图所示的三角形区域(包括边界)
解:不等式组表示的平面区域如图所示的三角形区域(包括边界)
z═x2+y2=(
)2表示平面区域内的点到原点(0,0)的距离的平方,由图象可知,
在A(1,1)处z取得最小值为2
故答案为:2.
 解:不等式组表示的平面区域如图所示的三角形区域(包括边界)
解:不等式组表示的平面区域如图所示的三角形区域(包括边界)z═x2+y2=(
| x2+y2 |
在A(1,1)处z取得最小值为2
故答案为:2.
点评:解题关键为z=x2+y2转化为平面区域内的点到原点(0,0)的距离的平方.

练习册系列答案
相关题目
已知集合A={0,1,2},B{1,2,3},则∁(A∪B)(A∩B)=( )
| A、{0,3} |
| B、{1,2} |
| C、∅ |
| D、{0,1,2,3} |
在长方体ABCD-A1B1C1D1中,AB=
,B1B=BC=1,则线BC1与面BDD1B1所成角的正弦为( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
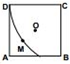
 如图,△ADP为正三角形,O为正方形ABCD中心,而ADP⊥面ABCD,M为面ABCD内的点,且满足MP=MC.则点M在正方形ABCD内的轨迹为( )
如图,△ADP为正三角形,O为正方形ABCD中心,而ADP⊥面ABCD,M为面ABCD内的点,且满足MP=MC.则点M在正方形ABCD内的轨迹为( )


 如图平行四边形ABCD中,∠DAB=60°,AB=2AD=2,M为边CD的中点,沿BM将△CBM折起使得平面BMC⊥平面ABMD.
如图平行四边形ABCD中,∠DAB=60°,AB=2AD=2,M为边CD的中点,沿BM将△CBM折起使得平面BMC⊥平面ABMD.