题目内容
已知函数f(x)=cosx-
sin(π-x).
(1)求函数f(x)的最小正周期和值域;
(2)若α是第二象限角,且f(α-
)=-
,试求
的值.
| 3 |
(1)求函数f(x)的最小正周期和值域;
(2)若α是第二象限角,且f(α-
| π |
| 3 |
| 2 |
| 3 |
| cos2α |
| 1+cos2α-sin2α |
考点:三角函数的周期性及其求法,三角函数的化简求值
专题:三角函数的图像与性质
分析:(1)由条件利用三角恒等变换求得f(x)=2cos(x+
),由此可得函数f(x)的最小正周期和值域.
(2)由条件利用三角恒等变换求得cosα、sin2α的值,从而求得
的值.
| π |
| 3 |
(2)由条件利用三角恒等变换求得cosα、sin2α的值,从而求得
| cos2α |
| 1+cos2α-sin2α |
解答:
解:(1)∵f(x)=cosx-
sin(π-x)=cosx-
sinx=2(
cosx-
sinx)=2cos(x+
),
∴函数f(x)的最小正周期T=2π,值域为[-2,2].
(2)由f(α-
)=-
得2cosα=-
,cosα=-
.
∵α是第二象限角,∴sinα=
=
=
,
∴cos2α=2cos2α-1=-
,sin2α=2sinαcosα=-
,
∴
=
=
.
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
∴函数f(x)的最小正周期T=2π,值域为[-2,2].
(2)由f(α-
| π |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
∵α是第二象限角,∴sinα=
| 1-cos2α |
1-
|
2
| ||
| 3 |
∴cos2α=2cos2α-1=-
| 7 |
| 9 |
4
| ||
| 9 |
∴
| cos2α |
| 1+cos2α-sin2α |
-
| ||||||
1-
|
1-2
| ||
| 2 |
点评:本题主要考查三角恒等变换,函数y=Asin(ωx+φ)的周期性,利用了函数y=Asin(ωx+φ)的周期为
,属于基础题.
| 2π |
| ω |

练习册系列答案
相关题目
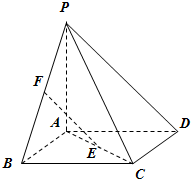 如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥底面ABCD,E,F分别是AC,PB的中点.求证:
如图,四棱锥P-ABCD的底面ABCD是正方形,PA⊥底面ABCD,E,F分别是AC,PB的中点.求证: