题目内容
设函数f(α)=
.
(1)设A是△ABC的内角,且为钝角,求f(A)的最小值;
(2)设A,B是锐角△ABC的内角,且A+B=
,f(A)=1,BC=2,求△ABC 的三个内角的大小和AC边的长.
(1+cos2α)cos(
| ||
| 2cos(π+α) |
(1)设A是△ABC的内角,且为钝角,求f(A)的最小值;
(2)设A,B是锐角△ABC的内角,且A+B=
| 7π |
| 12 |
考点:运用诱导公式化简求值,三角函数中的恒等变换应用,正弦定理
专题:解三角形
分析:(1)利用二倍角公式以及诱导公式化简函数的表达式,通过角的范围利用正弦函数的值域求出函数的最小值.
(2)通过A,B是锐角△ABC的内角,且A+B=
,f(A)=1,求出三个角的大小,结合BC=2,利用正弦定理,求出AC边的长.
(2)通过A,B是锐角△ABC的内角,且A+B=
| 7π |
| 12 |
解答:
解:(1)∵f(α)=
+cos2α=sinαcosα+cos2α
=
sin2α+
cos2α+
=
sin(2α+
)+
…(3分)
∵A是△ABC的内角,且为钝角,
∴A∈(
,π),∴2A+
∈(
,
)…(4分)
∴sin(2A+
)的最小值为-1,…(5分)
∴f(A)min=
…(6分)
(2)∵f(A)=
sin(2A+
)+
=1
∴sin(2A+
)=
…(7分)
∵A是锐角△ABC的内角∴A=
,
又∵A+B=
π
∴B=
,∴C=
π…(10分)
由BC=2及
=
可得
=
解得AC=
…(12分)
| 2cos2α•(-sinα) |
| -2cosα |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
∵A是△ABC的内角,且为钝角,
∴A∈(
| π |
| 2 |
| π |
| 4 |
| 5π |
| 4 |
| 9π |
| 4 |
∴sin(2A+
| π |
| 4 |
∴f(A)min=
1-
| ||
| 2 |
(2)∵f(A)=
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
∴sin(2A+
| π |
| 4 |
| ||
| 2 |
∵A是锐角△ABC的内角∴A=
| π |
| 4 |
又∵A+B=
| 7 |
| 12 |
∴B=
| π |
| 3 |
| 5 |
| 12 |
由BC=2及
| BC |
| sinA |
| AC |
| sinB |
可得
| 2 | ||
sin
|
| AC | ||
sin
|
解得AC=
| 6 |
点评:不考查正弦定理以及两角和与差的三角函数,二倍角公式的应用,考查计算能力.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
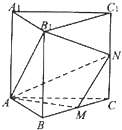 直三棱柱ABC-A1B1C1中,侧棱CC1=2,∠BAC=90°,AB=AC=
直三棱柱ABC-A1B1C1中,侧棱CC1=2,∠BAC=90°,AB=AC=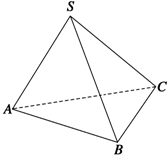 如图所示,在三棱锥S-ABC中,SA⊥SB,SB⊥SC,SA⊥SC,且SA、SB、SC和底面ABC所成的角分别为a1、a2、a3,三侧面△SBC、△SAC、△SAB的面积分别为S1、S2、S3,类比三角形中的正弦定理,给出空间情形的一个猜想.
如图所示,在三棱锥S-ABC中,SA⊥SB,SB⊥SC,SA⊥SC,且SA、SB、SC和底面ABC所成的角分别为a1、a2、a3,三侧面△SBC、△SAC、△SAB的面积分别为S1、S2、S3,类比三角形中的正弦定理,给出空间情形的一个猜想.