题目内容
设
=(1,
),
=(0,1),O为坐标原点,动点P(x,y)满足0≤
•
≤1,0≤
•
≤1,则z=
的最小值是 .
| OM |
| 1 |
| 2 |
| ON |
| OP |
| OM |
| OP |
| ON |
| y+3 |
| x+2 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:利用数量积运算可得0≤x+
y≤1,0≤y≤1.画出可行域如图所示,再利用斜率的计算公式即可得出.
| 1 |
| 2 |
解答:
解:∵
=(1,
),
=(0,1),O为坐标原点,动点P(x,y)满足0≤
•
≤1,
0≤
•
≤1,
∴0≤x+
y≤1,0≤y≤1.
画出可行域如图所示,
则z=
表示点Q(-2,-3)与可行域中的点P(x,y)连线的斜率.
A(1,0),C(-
,1).
∵kAQ=1,kCQ=
.
因此z=
的最小值是1.
故答案为:1.
| OM |
| 1 |
| 2 |
| ON |
| OP |
| OM |
0≤
| OP |
| ON |

∴0≤x+
| 1 |
| 2 |
画出可行域如图所示,
则z=
| y+3 |
| x+2 |
A(1,0),C(-
| 1 |
| 2 |
∵kAQ=1,kCQ=
| 8 |
| 3 |
因此z=
| y+3 |
| x+2 |
故答案为:1.
点评:本题考查了数量积运算、线性规划与可行域、斜率的计算公式等基础知识与基本技能方法,考查了转化方法和计算能力,属于中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
在一次防恐演习中,某射手击中目标的概率为0.8,每次射击的结果相互独立,现射击99次,则他最有可能射中目标( )次.
| A、99 | B、80 |
| C、79或80 | D、79 |
已知集合A={x|y=
},B={y|y=2x,x∈R},则A∩B=( )
| x-x2 |
| A、[0,1] |
| B、(0,1) |
| C、(0,1] |
| D、[0,1) |
 函数y=Asin(ωx+φ),(A,ω,φ为常数,A>0,ω>0)在闭区间[0,
函数y=Asin(ωx+φ),(A,ω,φ为常数,A>0,ω>0)在闭区间[0,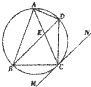 如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD∥MN,AC与BD相交于点E.若AB=6,BC=4,则DE=
如图,△ABC内接于⊙O,AB=AC,直线MN切⊙O于点C,弦BD∥MN,AC与BD相交于点E.若AB=6,BC=4,则DE=