题目内容
已知等比数列{an}的公比为q,且q<0,其中a1,3a3,a2成等差数列.
(Ⅰ)求q的值;
(Ⅱ)设{bn}是以2为首项,q为公差的等差数列,其前n项和为Sn,求使Sn>0成立的最大正整数n.
(Ⅰ)求q的值;
(Ⅱ)设{bn}是以2为首项,q为公差的等差数列,其前n项和为Sn,求使Sn>0成立的最大正整数n.
考点:等比数列的性质
专题:综合题,等差数列与等比数列
分析:(Ⅰ)由a1,3a3,a2成等差数列知6a3=a1+a2,即6a1q2=a1+a1q,解方程可求q;
(Ⅱ)利用等差数列的求和公式可求Sn,令Sn>0可求n的范围,结合n∈N*,即可得出结论.
(Ⅱ)利用等差数列的求和公式可求Sn,令Sn>0可求n的范围,结合n∈N*,即可得出结论.
解答:
解:(Ⅰ)由a1,3a3,a2成等差数列知6a3=a1+a2,
即6a1q2=a1+a1q,
所以6q2-q-1=0,
因为q<0,
所以q=-
;
(Ⅱ)Sn=2n+
•(-
)=
,
所以-n2+13n>0,解得0<n<13,
所以满足条件的最大值为n=12.
即6a1q2=a1+a1q,
所以6q2-q-1=0,
因为q<0,
所以q=-
| 1 |
| 3 |
(Ⅱ)Sn=2n+
| n(n-1) |
| 2 |
| 1 |
| 3 |
| -n2+13n |
| 6 |
所以-n2+13n>0,解得0<n<13,
所以满足条件的最大值为n=12.
点评:本题主要考查了等差数列的性质,考查等差数列与等比数列的综合应用,等差数列的求和公式的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
《张丘建算经》卷上第22题--“女子织布”问题:某女子善于织布,一天比一天织得快,而且每天增加的数量相同.已知第一天织布5尺,30天共织布390尺,则该女子织布每天增加( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合 A={x|x2+x-2<0},B={-2,-1,0,1,2},则A∩B=( )
| A、{-2,-1,0,1} |
| B、{-1,0,1} |
| C、{0,1} |
| D、{-1,0} |
 某教育主管部门到一所中学检查学生的体质健康情况.从全体学生中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式表示如图所示.根据学生体质健康标准,成绩不低于76的为优良.
某教育主管部门到一所中学检查学生的体质健康情况.从全体学生中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式表示如图所示.根据学生体质健康标准,成绩不低于76的为优良.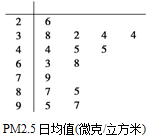 通常把大气中直径小于或等于2.5微米的颗粒物(也称为可入肺颗粒物)称为PM2.5.我国PM2.5标准采用世卫组织设定的最宽限值,空气质量与PM2.5的关系如下表:
通常把大气中直径小于或等于2.5微米的颗粒物(也称为可入肺颗粒物)称为PM2.5.我国PM2.5标准采用世卫组织设定的最宽限值,空气质量与PM2.5的关系如下表: