题目内容
设等比数列{an}的前n项和为Sn，已知S4=8，S8=12，则a13+a14+a15+a16的值为 ．
考点：等比数列的性质
专题：等差数列与等比数列
分析：由等比数列的性质可得S4，S8-S4，S12-S8，S16-S12成等比数列，由已知可得答案．
解答：
解：由等比数列的性质可得S4，S8-S4，S12-S8，S16-S12成等比数列，
由已知可得S4=8，S8-S4=12-8=4，
∴S12-S8=2，S16-S12=1，
即a13+a14+a15+a16=S16-S12=1
故答案为：1
由已知可得S4=8，S8-S4=12-8=4，
∴S12-S8=2，S16-S12=1，
即a13+a14+a15+a16=S16-S12=1
故答案为：1
点评：本题考查等比数列的性质，“判断和”成等比数列是解决问题的关键，属中档题．
练习册系列答案
名校课堂系列答案
相关题目
已知变量x，y满足不等式组
，则z=2x+2y的最小值为（ ）
|
A、
| |||||
| B、2 | |||||
C、3
| |||||
D、3
|
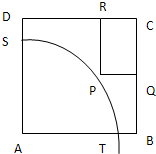如图：ABCD是一个边长为100m的正方形地皮，其中AST是一个半径为90m的扇形小山，其余部分都是平地，政府为方便附近住户，计划在平地上建立一个矩形停车场，使矩形的一个顶点P在弧
设函数f（x）=alnx+blgx+1，则f（1）+f（2）+…+f（2014）+f（
）+f（
）+…+f（
）=（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2014 |
| A、4028 | B、4027 |
| C、2014 | D、2013 |
已知函数f（x）=x2+f′（2）（lnx-x），则f′（1）=（ ）
| A、1 | B、2 | C、3 | D、4 |