题目内容
 某教育主管部门到一所中学检查学生的体质健康情况.从全体学生中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式表示如图所示.根据学生体质健康标准,成绩不低于76的为优良.
某教育主管部门到一所中学检查学生的体质健康情况.从全体学生中,随机抽取12名进行体质健康测试,测试成绩(百分制)以茎叶图形式表示如图所示.根据学生体质健康标准,成绩不低于76的为优良.(Ⅰ)写出这组数据的众数和中位数;
(Ⅱ)将频率视为概率.根据样本估计总体的思想,在该校学生中任选3人进行体质健康测试,求至少有1人成绩是“优良”的概率;
(Ⅲ)从抽取的12人中随机选取3人,记ξ表示成绩“优良”的学生人数,求ξ的分布列及期望.
考点:离散型随机变量的期望与方差,众数、中位数、平均数,古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)利用茎叶图能求出这组数据的众数,中位数.
(Ⅱ)抽取的12人中成绩是“优良”的频率为
,由此得到从该校学生中任选1人,成绩是“优良”的概率为
,从而能求出“在该校学生中任选3人,至少有1人成绩是‘优良’”的概率.
(Ⅲ)由题意可得,ξ的可能取值为0,1,2,3,分别求出相对应的概率,由此能求出ξ的分布列和Eξ.
(Ⅱ)抽取的12人中成绩是“优良”的频率为
| 3 |
| 4 |
| 3 |
| 4 |
(Ⅲ)由题意可得,ξ的可能取值为0,1,2,3,分别求出相对应的概率,由此能求出ξ的分布列和Eξ.
解答:
解:(Ⅰ)这组数据的众数为86,中位数为86.…(4分)
(Ⅱ)抽取的12人中成绩是“优良”的频率为
,
故从该校学生中任选1人,成绩是“优良”的概率为
,…(5分)
设“在该校学生中任选3人,至少有1人成绩是‘优良’的事件”为A,
则P(A)=1-
×(1-
)3=1-
=
.…(7分)
(Ⅲ)由题意可得,ξ的可能取值为0,1,2,3.…(8分)
P(ξ=0)=
=
,P(ξ=1)=
=
,
P(ξ=2)=
=
=
,P(ξ=3)=
=
=
,
所以ξ的分布列为
…(12分)
Eξ=0×
+1×
+2×
+3×
=
.…(13分)
(Ⅱ)抽取的12人中成绩是“优良”的频率为
| 3 |
| 4 |
故从该校学生中任选1人,成绩是“优良”的概率为
| 3 |
| 4 |
设“在该校学生中任选3人,至少有1人成绩是‘优良’的事件”为A,
则P(A)=1-
| C | 0 3 |
| 3 |
| 4 |
| 1 |
| 64 |
| 63 |
| 64 |
(Ⅲ)由题意可得,ξ的可能取值为0,1,2,3.…(8分)
P(ξ=0)=
| ||
|
| 1 |
| 220 |
| ||||
|
| 27 |
| 220 |
P(ξ=2)=
| ||||
|
| 108 |
| 220 |
| 27 |
| 55 |
| ||
|
| 84 |
| 220 |
| 21 |
| 55 |
所以ξ的分布列为
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
Eξ=0×
| 1 |
| 220 |
| 27 |
| 220 |
| 27 |
| 55 |
| 21 |
| 55 |
| 9 |
| 4 |
点评:本小题主要考查茎叶图、众数、中位数、随机变量的分布列、期望等基础知识,考查数据处理能力、运算求解能力以及应用意识,考查必然与或然思想等.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
下列哪个函数的图象只需平移变换即可得到f(x)=sinx+cosx的函数图象( )
A、f1(x)=
| ||||||||
| B、f2(x)=sinx | ||||||||
C、f3(x)=
| ||||||||
D、f4(x)=
|
已知变量x,y满足不等式组
,则z=2x+2y的最小值为( )
|
A、
| |||||
| B、2 | |||||
C、3
| |||||
D、3
|
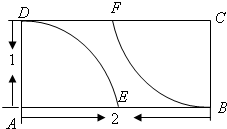 如图,在矩形区域ABCD的A,C两点处各有一个通信基站,假设其信号覆盖范围分别是扇形区域ADE和扇形区域CBF(该矩形区域内无其他信号来源,基站工作正常).若在该矩形区域内随机地选一地点,则该地点无信号的概率是
如图,在矩形区域ABCD的A,C两点处各有一个通信基站,假设其信号覆盖范围分别是扇形区域ADE和扇形区域CBF(该矩形区域内无其他信号来源,基站工作正常).若在该矩形区域内随机地选一地点,则该地点无信号的概率是