题目内容
若函数y=f(x)(x∈D)同时满足下列条件:
①f(x)在D内为单调函数;
②f(x)的值域为D的子集,则称此函数为D内的“保值函数”.
(Ⅰ)f(x)=
是[1,+∞)内的“保值函数”,则b的最小值为 ;
(Ⅱ)当-1≤a≤1,且a≠0,-1≤b≤1时,g(x)=ax2+b是[0,1]内的“保值函数”的概率为 .
①f(x)在D内为单调函数;
②f(x)的值域为D的子集,则称此函数为D内的“保值函数”.
(Ⅰ)f(x)=
| 2x+b-4 |
| ln2 |
(Ⅱ)当-1≤a≤1,且a≠0,-1≤b≤1时,g(x)=ax2+b是[0,1]内的“保值函数”的概率为
考点:几何概型,利用导数研究函数的单调性
专题:综合题,概率与统计
分析:(Ⅰ)由求导判断可得f(x)为增函数,进而可得f(x)的值域,根据题意中保值函数的定义,可得
≥1,解可得b的范围,即可得答案.
(Ⅱ)根据题意,由a、b的范围分析可得其表示的平面区域,计算可得其面积,对于函数f(x),分-1≤a<0与0<a≤1两种情况,先分析出f(x)的单调性,由此得到f(x)的值域,进而由保值函数的定义,可得关于a、b的不等式组,分析可得其对应的平面区域,易得其面积,综合两种情况可得f(x)为保值函数对应的平面区域即面积,由几何概型公式计算可得答案.
| b-2 |
| ln2 |
(Ⅱ)根据题意,由a、b的范围分析可得其表示的平面区域,计算可得其面积,对于函数f(x),分-1≤a<0与0<a≤1两种情况,先分析出f(x)的单调性,由此得到f(x)的值域,进而由保值函数的定义,可得关于a、b的不等式组,分析可得其对应的平面区域,易得其面积,综合两种情况可得f(x)为保值函数对应的平面区域即面积,由几何概型公式计算可得答案.
解答:
解:(Ⅰ)根据题意,f′(x)=2x>0,则f(x)在[1,+∞)为增函数,
故f(x)的最小值为f(1)=
,其最大值不存在,则f(x)的值域为[
,+∞),
又由f(x)在[1,+∞)是“保值函数”,
则有
≥1,解可得b≥2+ln2;
故b的最小值为2+ln2.
(Ⅱ)根据题意,-1≤a≤1,且a≠0,-1≤b≤1,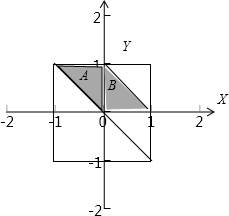
则a、b确定的区域为边长为2的正方形,其面积为4;
对于f(x),有f′(x)=2ax,x∈[0,1],
当-1≤a<0时,f′(x)<0,f(x)为减函数,
则f(x)的最大值为f(0)=b,最小值为f(1)=a+b,则f(x)的值域为[a+b,a],
若f(x)为保值函数,则有
,
其表示的区域为阴影三角形A,面积为
,
当0<a≤1时,f′(x)>0,f(x)为增函数,
则f(x)的最小值为f(0)=b,最大值为f(1)=a+b,则f(x)的值域为[a,a+b],
若f(x)为保值函数,则有
,
其表示的区域为阴影三角形B,面积为
;
f(x)为保值函数对应区域的面积为1;
则f(x)为保值函数的概率为
;
故答案为:2+ln2;
.
故f(x)的最小值为f(1)=
| b-2 |
| ln2 |
| b-2 |
| ln2 |
又由f(x)在[1,+∞)是“保值函数”,
则有
| b-2 |
| ln2 |
故b的最小值为2+ln2.
(Ⅱ)根据题意,-1≤a≤1,且a≠0,-1≤b≤1,

则a、b确定的区域为边长为2的正方形,其面积为4;
对于f(x),有f′(x)=2ax,x∈[0,1],
当-1≤a<0时,f′(x)<0,f(x)为减函数,
则f(x)的最大值为f(0)=b,最小值为f(1)=a+b,则f(x)的值域为[a+b,a],
若f(x)为保值函数,则有
|
其表示的区域为阴影三角形A,面积为
| 1 |
| 2 |
当0<a≤1时,f′(x)>0,f(x)为增函数,
则f(x)的最小值为f(0)=b,最大值为f(1)=a+b,则f(x)的值域为[a,a+b],
若f(x)为保值函数,则有
|
其表示的区域为阴影三角形B,面积为
| 1 |
| 2 |
f(x)为保值函数对应区域的面积为1;
则f(x)为保值函数的概率为
| 1 |
| 4 |
故答案为:2+ln2;
| 1 |
| 4 |
点评:本题考查几何概型的计算以及函数单调性的应用,关键是理解保值函数的定义.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列哪个函数的图象只需平移变换即可得到f(x)=sinx+cosx的函数图象( )
A、f1(x)=
| ||||||||
| B、f2(x)=sinx | ||||||||
C、f3(x)=
| ||||||||
D、f4(x)=
|
命题p:?x∈R,sinx-cosx<
,命题q:“a=1”是“直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0平行”的充分条件,则下列命题中,真命题是( )
| 2 |
| A、(¬q)∨p |
| B、p∧q |
| C、(¬p)∧(¬q) |
| D、(¬p)∨(¬q) |
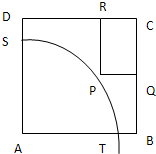 如图:ABCD是一个边长为100m的正方形地皮,其中AST是一个半径为90m的扇形小山,其余部分都是平地,政府为方便附近住户,计划在平地上建立一个矩形停车场,使矩形的一个顶点P在弧
如图:ABCD是一个边长为100m的正方形地皮,其中AST是一个半径为90m的扇形小山,其余部分都是平地,政府为方便附近住户,计划在平地上建立一个矩形停车场,使矩形的一个顶点P在弧