题目内容
泉州某鱼苗养殖户,由于受养殖技术水平和环境等因素的制约,会出现一些鱼苗的死亡,根据以往经验,鱼苗的死亡数p(万条)与月养殖数x(万条)之间满足关系:P=
,已知每成活1万条鱼苗可以盈利2万元,但每死亡1万条鱼苗讲亏损1万元.
(Ⅰ)试将该养殖户每月养殖鱼苗所获得的利润T(万元)表示为月养殖量x(万条的函数);
(Ⅱ)该养殖户鱼苗的月养殖量是多少时获得的利润最大,最大利润是多少?(利润=盈利-亏损)
|
(Ⅰ)试将该养殖户每月养殖鱼苗所获得的利润T(万元)表示为月养殖量x(万条的函数);
(Ⅱ)该养殖户鱼苗的月养殖量是多少时获得的利润最大,最大利润是多少?(利润=盈利-亏损)
考点:分段函数的应用
专题:综合题,函数的性质及应用
分析:(1)由已知中鱼苗的死亡数p(万条)与月养殖数x(万条)之间满足关系式,可求出成活的鱼苗数,进而根据每成活1万条鱼苗可以盈利2万元,但每死亡1万条鱼苗讲亏损1万元,得到利润T(万元)与月养殖量的函数解析式.
(2)由(1)中结论,结合二次函数的图象和性质,可以求出月养殖量x定为多少时获得的利润最大,及最大利润值.
(2)由(1)中结论,结合二次函数的图象和性质,可以求出月养殖量x定为多少时获得的利润最大,及最大利润值.
解答:
解:(1)当1≤x<4时,成活的鱼苗数为x-
,…(1分)
利润T=2(x-
)-
=2x-
…(3分)
当x≥4时,成活的鱼苗数为x-(x+
-
)=-
+
,…(4分)
利润T=2(-
+
)-(x+
-
)=-x-
+
,…(6分)
综上,该工厂每天生产这种元件所获得的利润T=
…(7分)
(2)当1≤x<4时,T=2x-
,对称轴x=2,此时利润T的最大值Tmax=T(2)=2.…(9分)
当x≥4时,T′=
<0,…(10分)
所以T=-x-
+
在[4,+∞)上是减函数,…(11分)
此时利润T的最大值Tmax=T(4)=0,…(12分)
综上所述,当x=2时,T取最大值2,…(13分)
即当养殖户鱼苗的月养殖量定为2(万件)时,可获得最大利润2万元.…(14分)
| x2 |
| 6 |
利润T=2(x-
| x2 |
| 6 |
| x2 |
| 6 |
| x2 |
| 2 |
当x≥4时,成活的鱼苗数为x-(x+
| 3 |
| x |
| 25 |
| 12 |
| 3 |
| x |
| 25 |
| 12 |
利润T=2(-
| 3 |
| x |
| 25 |
| 12 |
| 3 |
| x |
| 25 |
| 12 |
| 9 |
| x |
| 25 |
| 4 |
综上,该工厂每天生产这种元件所获得的利润T=
|
(2)当1≤x<4时,T=2x-
| x2 |
| 2 |
当x≥4时,T′=
| (3+x)(3-x) |
| x2 |
所以T=-x-
| 9 |
| x |
| 25 |
| 4 |
此时利润T的最大值Tmax=T(4)=0,…(12分)
综上所述,当x=2时,T取最大值2,…(13分)
即当养殖户鱼苗的月养殖量定为2(万件)时,可获得最大利润2万元.…(14分)
点评:本题考查的知识点是根据实际问题选择函数类型,熟练掌握二次函数的图象和性质是解答的关键.

练习册系列答案
相关题目
已知x>y>z,且x+y+z=1.下列不等式中成立的是( )
| A、xy>yz |
| B、xy>xz |
| C、xz>yx |
| D、x|y|>z|y| |
函数f(x)=2x-cosx在(-∞,+∞)上( )
| A、有最大值 | B、无最大值 |
| C、有最小值 | D、无最值 |
已知等差数列{an}中,a1+a3=a4=8,则a6的值是( )
| A、10 | B、12 | C、8 | D、16 |
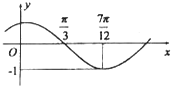 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<