题目内容
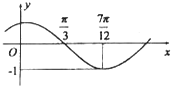函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜| π |
| 2 |
（1）求函数f（x）的解析式．
（2）为了得到g（x）=cos2x的图象，则只要将f（x）的图象怎样进行变换．
考点：由y=Asin（ωx+φ）的部分图象确定其解析式,函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：（1）由函数的图象的顶点坐标求出A，由周期求出ω，由五点法作图求出φ的值，从而求得函数的解析式．
（2）利用诱导公式可得f（x）=cos2（x-
），再根据函数y=Asin（ωx+φ）的图象变换规律，可得结论．
（2）利用诱导公式可得f（x）=cos2（x-
| π |
| 12 |
解答：
解：（1）由函数的图象可得 A=1，由
=
•
=
-
，可得ω=2．
再根据五点法作图可得 2×
+φ=π 求得 φ=
，
故函数的解析式为 f(x)=sin(2x+
)．
（2）∵f（x）=sin（2x+
）=cos（
-2x）=cos2（x-
），
故将f（x）的图象向左平移
个单位，即可得到g（x）=cos2x的图象．
| T |
| 4 |
| 1 |
| 4 |
| 2π |
| ω |
| 7π |
| 12 |
| π |
| 3 |
再根据五点法作图可得 2×
| π |
| 3 |
| π |
| 3 |
故函数的解析式为 f(x)=sin(2x+
| π |
| 3 |
（2）∵f（x）=sin（2x+
| π |
| 3 |
| π |
| 6 |
| π |
| 12 |
故将f（x）的图象向左平移
| π |
| 12 |
点评：本题主要考查由函数y=Asin（ωx+φ）的部分图象求解析式，诱导公式，函数y=Asin（ωx+φ）的图象变换规律，统一这两个三角函数的名称，是解题的关键，属于基础题．
练习册系列答案
相关题目
某个公园有个池塘，其形状为直角三角形ABC，∠C=90°，AB=100米，BC=50米．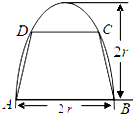
如图，有一块半椭圆形钢板，其长半轴长为2r，短半轴长为r，计划将此钢板切割成等腰梯形的形状，下底AB是半椭圆的短轴，上底CD的端点在椭圆上，记CD=2x，梯形面积为S．
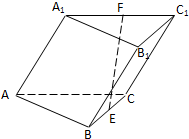如图，斜三棱柱ABC-A1B1C1的侧棱长为
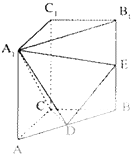直三棱柱ABC-A1B1C1中，AC=CB=AA1=2，∠ACB=90°，E是BB1的中点，D∈AB，∠A1DE=90°．