题目内容
已知函数f(x)=eax-x,其中a≠0,函数f(x)的导函数是f′(x).
(I)若对一切x∈R,f(x)≥1恒成立,求a的取值范围;
(Ⅱ)是否存在实数a,使函数g(x)=|
|在区间(0,4)内的图象上存在两点,在该两点处的切线互相垂直?若存在,求出a的取值范围;若不存在,请说明理由?
(I)若对一切x∈R,f(x)≥1恒成立,求a的取值范围;
(Ⅱ)是否存在实数a,使函数g(x)=|
| ln[f′(x)+1]-lna-a2 |
| ln[f′(x)+1]-lna+2a2 |
考点:利用导数求闭区间上函数的最值,导数的运算,利用导数研究曲线上某点切线方程
专题:综合题,导数的综合应用
分析:(I)可判断a<0时不等式不成立,从而得知a>0,则问题转化为f(x)min≥1,利用导数可求得f(x)min=
-
ln
,进而通过构造函数利用导数可解不等式;
(Ⅱ)要存在x1,x2∈(0,4)(x1<x2),使曲线y=g(x)在(x1,g(x1),(x2,g(x2))两点处的切线互相垂直,须g′(x1)•g(′(x2)=-1,根据导数的符号可判断,有a>4,且x1∈(0,a),x2∈(a,4),而g′(x1)•g′(x2)=-1⇒x1+2a=
①,由x1+2a∈(2a,3a),
∈(
,1)知,问题等价于集合A={x|2a<x<3a}与集合B={x|
<x<1}的交集非空,借助数轴可得不等式;
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
(Ⅱ)要存在x1,x2∈(0,4)(x1<x2),使曲线y=g(x)在(x1,g(x1),(x2,g(x2))两点处的切线互相垂直,须g′(x1)•g(′(x2)=-1,根据导数的符号可判断,有a>4,且x1∈(0,a),x2∈(a,4),而g′(x1)•g′(x2)=-1⇒x1+2a=
| 3a |
| x2+2a |
| 3a |
| x2+2a |
| 3a |
| 4+2a |
| 3a |
| 4+2a |
解答:
解:(I)若a<0则对一切x>0,f(x)=eax-x<1这与题设矛盾;
又a≠0,故a>0,
f′(x)=aeax-1,f′(x)=0⇒x=
ln
,
当x<
ln
,f′(x)<0,f(x)单调递减,当x>
ln
,f′(x)>0,f(x)单调递增;
故当x=
ln
时,f(x)min=f(
ln
)=
-
ln
,
对一切x∈R,f(x)≥1恒成立,当且仅当
-
ln
≥1①,
令g(t)=t-tlnt,g′(t)=-lnt,
当0<t<1时,g′(t)>0,当t>1时,g′(t)<0,
∴当t=1时,g(t)max=g(1)=1,
当且仅当
=1⇒a=1时,(1)式成立,
∴a的取值集合是{1}.
(Ⅱ)g(x)=|
|,
当x∈(0,a),g(x)=
,g′(x)=
<0,g(x)递减,
当x∈(a,+∞),g(x)=
,g′(x)=
>0,g(x)递增,
若a>4,g(x)在(0,4)上递减,故不满足要求;
当a<4,g(x)在(0,a)上递减,在(a,4)上递增,
若存在x1,x2∈(0,4)(x1<x2),使曲线y=g(x)在(x1,g(x1),(x2,g(x2))两点处的切线互相垂直,
则x1∈(0,a),x2∈(a,4),
且g′(x1)•g(′(x2)=-1⇒
•
=-1⇒x1+2a=
①,
由x1∈(0,a)⇒x1+2a∈(2a,3a),x2∈(a,4)⇒
∈(
,1),
故①式成立,等价于集合A={x|2a<x<3a}与集合B={x|
<x<1}的交集非空,
又
<3a,当且仅当0<2a<1即0<a<
时,A∩B≠∅,
所以a的取值范围是(0,
).
又a≠0,故a>0,
f′(x)=aeax-1,f′(x)=0⇒x=
| 1 |
| a |
| 1 |
| a |
当x<
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
故当x=
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
对一切x∈R,f(x)≥1恒成立,当且仅当
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
令g(t)=t-tlnt,g′(t)=-lnt,
当0<t<1时,g′(t)>0,当t>1时,g′(t)<0,
∴当t=1时,g(t)max=g(1)=1,
当且仅当
| 1 |
| a |
∴a的取值集合是{1}.
(Ⅱ)g(x)=|
| x-a |
| x+2a |
当x∈(0,a),g(x)=
| -x+a |
| x+2a |
| -3a |
| (x+2a)2 |
当x∈(a,+∞),g(x)=
| x-a |
| x+2a |
| 3a |
| (x+2a)2 |
若a>4,g(x)在(0,4)上递减,故不满足要求;
当a<4,g(x)在(0,a)上递减,在(a,4)上递增,
若存在x1,x2∈(0,4)(x1<x2),使曲线y=g(x)在(x1,g(x1),(x2,g(x2))两点处的切线互相垂直,
则x1∈(0,a),x2∈(a,4),
且g′(x1)•g(′(x2)=-1⇒
| -3a |
| (x1+2a)2 |
| 3a |
| (x2+2a)2 |
| 3a |
| x2+2a |
由x1∈(0,a)⇒x1+2a∈(2a,3a),x2∈(a,4)⇒
| 3a |
| x2+2a |
| 3a |
| 4+2a |
故①式成立,等价于集合A={x|2a<x<3a}与集合B={x|
| 3a |
| 4+2a |
又
| 3a |
| 4+2a |
| 1 |
| 2 |
所以a的取值范围是(0,
| 1 |
| 2 |
点评:该题考查导数的运算、几何意义以及利用导数研究函数的最值、函数恒成立等知识,考查转化思想,考查学生综合运用知识分析问题解决问题的能力.

练习册系列答案
相关题目
不等式x2+x-6≤0的解集是( )
| A、{x|x≥x-3} |
| B、{x|-2≤x≤3} |
| C、{x|x≤2} |
| D、{x|-3≤x≤2} |
 在一项农业试验中,为了比较两种肥料对于某种果树的施肥效果,随机选取了施用这两种肥料的果树各10棵的产量(单位:kg):
在一项农业试验中,为了比较两种肥料对于某种果树的施肥效果,随机选取了施用这两种肥料的果树各10棵的产量(单位:kg): 某个公园有个池塘,其形状为直角三角形ABC,∠C=90°,AB=100米,BC=50米.
某个公园有个池塘,其形状为直角三角形ABC,∠C=90°,AB=100米,BC=50米.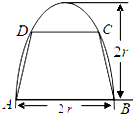 如图,有一块半椭圆形钢板,其长半轴长为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S.
如图,有一块半椭圆形钢板,其长半轴长为2r,短半轴长为r,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记CD=2x,梯形面积为S.