题目内容
已知f（x）=logax，g（x）=loga（2-x），（a＞0，a≠1），
（1）若f（4）＜2，求a的取值范围；
（2）若a＞1，设h（x）=f（x）+g（x），求h（x）的定义域和值域．
（1）若f（4）＜2，求a的取值范围；
（2）若a＞1，设h（x）=f（x）+g（x），求h（x）的定义域和值域．
考点：函数的值域,函数的定义域及其求法
专题：函数的性质及应用
分析：（1）由f（4）＜2得loga4＜2，讨论a＞1、0＜a＜1时，a的取值范围；
（2）由对数的真数大于0求出x的取值范围，由函数对应关系得出h（x）的取值范围，即得定义域和值域．
（2）由对数的真数大于0求出x的取值范围，由函数对应关系得出h（x）的取值范围，即得定义域和值域．
解答：
解：（1）由f（4）＜2得，loga4＜2；
若a＞1，则a2＞4，解得，a＞2；（3分）
若0＜a＜1，则a2＜4，解得，0＜a＜1；（6分）
综上所述：a＞2或0＜a＜1；（7分）
（2）h（x）=logax+loga（2-x）=loga（-x2+2x），（a＞1）；
则
，解得，0＜x＜2；（10分）
又∵-x2+2x∈（0，1]；
∴h（x）∈（-∞，0]；（13分）
∴h（x）的定义域为（0，2），值域为（-∞，0]．（14分）
若a＞1，则a2＞4，解得，a＞2；（3分）
若0＜a＜1，则a2＜4，解得，0＜a＜1；（6分）
综上所述：a＞2或0＜a＜1；（7分）
（2）h（x）=logax+loga（2-x）=loga（-x2+2x），（a＞1）；
则
|
又∵-x2+2x∈（0，1]；
∴h（x）∈（-∞，0]；（13分）
∴h（x）的定义域为（0，2），值域为（-∞，0]．（14分）
点评：本题考查了函数的定义域与值域的问题，解题时应根据函数的解析式求出函数的定义域和值域，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
设a＞0，b＞0，且4a+b=3ab，则a+4b的最小值是（ ）
| A、8 | ||
B、
| ||
| C、9 | ||
D、
|
已知直线l经过点M（-1，2），且倾斜角为
，则直线l的一个参数方程为（其中t为参数）（ ）
| π |
| 6 |
A、
| |||||||||||
B、
| |||||||||||
C、
| |||||||||||
D、
|
在一项农业试验中，为了比较两种肥料对于某种果树的施肥效果，随机选取了施用这两种肥料的果树各10棵的产量（单位：kg）：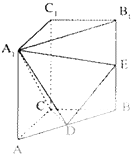
直三棱柱ABC-A1B1C1中，AC=CB=AA1=2，∠ACB=90°，E是BB1的中点，D∈AB，∠A1DE=90°．