题目内容
下列命题错误的是( )
| A、若p或q为假命题,则p,q均为假命题 |
| B、命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” |
| C、若某一集合有4个元素,那么它真子集的个数共有24个 |
| D、?x∈Z,x3<1 |
考点:命题的真假判断与应用
专题:阅读型,集合,简易逻辑
分析:由复合命题的真假,即可判断A;由逆否命题的写法:先逆后否,即可判断B;
由n个元素的集合的真子集个数为2n-1,即可判断C;可举反例,比如x=0,即可判断D.
由n个元素的集合的真子集个数为2n-1,即可判断C;可举反例,比如x=0,即可判断D.
解答:
解:A.若p或q为假命题,则p,q均为假,故A正确;
B.命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”,故B正确;
C.若某一集合有4个元素,则它的子集个数为24=16,真子集个数为24-1=15.故C错;
D.若x=0,则03<1,故D正确.
故选C.
B.命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0”,故B正确;
C.若某一集合有4个元素,则它的子集个数为24=16,真子集个数为24-1=15.故C错;
D.若x=0,则03<1,故D正确.
故选C.
点评:本题考查四种命题及真假的判断,存在性命题的判断,考查集合的子集和真子集的个数,属于基础题.

练习册系列答案
相关题目
若直线
(t为参数)与直线4x+ky=1垂直,则常数k=( )
|
| A、7 | B、5 | C、4 | D、6 |
已知数列{an}为等比数列,a4+a7=2,a5•a6=-8,则a1+a10的值为( )
| A、7 | B、-5 | C、5 | D、-7 |
已知函数f(x)=x3+3mx2+nx+m2在x=-1时有极值为0,则m+n=( )
| A、11 | B、4或11 | C、4 | D、8 |
在R上可导的函数f(x)的图形如图所示,则关于x的不等式x•f′(x)<0的解集为( )
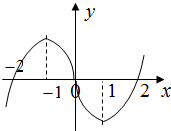
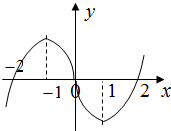
| A、(-∞,-1)∪(0,1) |
| B、(-1,0)∪(1,+∞) |
| C、(-2,-1)∪(1,2) |
| D、(-∞,-2)∪(2,+∞) |
下列参数方程与方程y=2x表示相同图象的是( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
函数y=
sin(2x-
)的图象可以看作是函数y=
sin2x的图象( )
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
函数y=sin(-x+
)在x∈[0,2π]的一个单调递增区间是( )
| π |
| 4 |
A、[0,
| ||||
B、[
| ||||
C、[
| ||||
D、[
|