题目内容
 实数x,y满足
实数x,y满足
|
(Ⅰ)求z=
| y |
| x+1 |
(Ⅱ)若函数z=ax+by(a>0,b>0)的最大值为3,求t=a•(1+b)的最大值.
考点:简单线性规划
专题:不等式的解法及应用
分析:(Ⅰ)画出不等式组表示的可行域,利用z=
的几何意义,求出它的取值范围;
(Ⅱ)转化函数z=ax+by(a>0,b>0)的斜率,利用几何意义通过最大值为3,得到2a+b=3,利用基本不等式求t=a•(1+b)的最大值.
| y |
| x+1 |
(Ⅱ)转化函数z=ax+by(a>0,b>0)的斜率,利用几何意义通过最大值为3,得到2a+b=3,利用基本不等式求t=a•(1+b)的最大值.
解答:
 (本小题满分14分)
(本小题满分14分)
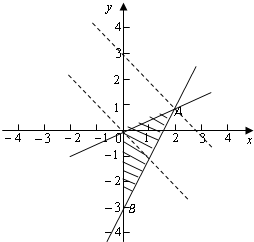
解:( I)做可行域如图中阴影所示.
设P(x,y)为可行域内任一点,M(-1,0).
则z=
=kPM…1分.
A(2,1),B(0,-3),kMB=-3, kMA=
…1分
∴z=
∈[-3,
]….2分.
( II)z=ax+by?y=-
x+
z
表示一族斜率为-
(<0),纵截距为
z的平行直线 …1分.
当直线过点A(2,1)时,纵截距最大,z也取最大,zmax=2a+b=3…2分.
t=a•(1+b)=2a•(1+b)×
≤(
)2×
=2….2分.
取“=”当且仅当
即
…..1分.
∴tmax=2…1分.
 (本小题满分14分)
(本小题满分14分)解:( I)做可行域如图中阴影所示.
设P(x,y)为可行域内任一点,M(-1,0).
则z=
| y |
| x+1 |
A(2,1),B(0,-3),kMB=-3, kMA=
| 1 |
| 3 |
∴z=
| y |
| x+1 |
| 1 |
| 3 |
( II)z=ax+by?y=-
| a |
| b |
| 1 |
| b |
表示一族斜率为-
| a |
| b |
| 1 |
| b |
当直线过点A(2,1)时,纵截距最大,z也取最大,zmax=2a+b=3…2分.
t=a•(1+b)=2a•(1+b)×
| 1 |
| 2 |
| 2a+1+b |
| 2 |
| 1 |
| 2 |
取“=”当且仅当
|
|
∴tmax=2…1分.
点评:本题考查线性规划的应用,基本上求解表达式的最值,考查分析问题解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知0<t≤
,那么
-t的最小值是( )
| 1 |
| 4 |
| 1 |
| t |
A、
| ||
B、
| ||
| C、2 | ||
| D、-2 |
已知椭圆:
+
=1的焦距为4,则m等于( )
| x2 |
| 10-m |
| y2 |
| m-2 |
| A、4 | B、8 |
| C、4或8 | D、以上均不对 |
设集合M={x|0≤x≤2},N={y|0≤y≤2},给出下列4个图形,其中能表示集合M到N的函数关系的有( )
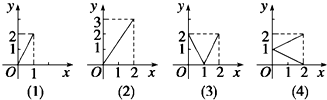

| A、0个 | B、1个 | C、2个 | D、3个 |
设圆C1:(x-1)2+y2=1与圆C2:(x-3)2+(y-2)2=1,点P为一动点,由点P作圆C1与圆C2的切线PA,PB,切点分别为A,B.若|PA|=|PB|,则点P的轨迹方程为( )
| A、x+y-3=0 |
| B、x+y+3=0 |
| C、x-y+3=0 |
| D、x-y-3=0 |