题目内容
 函数f(x)=2
函数f(x)=2| 3 |
| ωx |
| 2 |
| ωx |
| 2 |
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)将f(x)的图象上每个点的横坐标缩小为原来的
| π |
| 4 |
| π |
| 3 |
考点:三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(Ⅰ)化简可得f(x)=2
sin(ωx+
),由|BC|=4可求得ω=
,从而确定函数f(x)的解析式;
(Ⅱ)由OP⊥OQ得
θ+2
•2
sinθ=0,即πθ+24sinθ=0(π<θ<2π),问题转化为研讨函数h(x)=πx+24sinx(π<x<2π)零点个数,根据零点判定定理即可求得.
| 3 |
| π |
| 3 |
| π |
| 4 |
(Ⅱ)由OP⊥OQ得
| π |
| 2 |
| 3 |
| 3 |
解答:
解:(1)由已知得:f(x)=2
sin
•cos
+3cosωx=
sinωx+3cosωx
=2
sin(ωx+
)
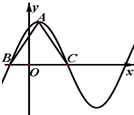
∵A为图象的最高点,∴A的纵坐标为2
又∵△ABC为正三角形,所以|BC|=4
∴
=4可得T=8即
=8得ω=
∴f(x)=2
sin(
x+
)
(2)由题意可得g(x)=2
sinx,P(
,2
)
法一:作出如右图象,由图象可知满足条件的点Q是存在的,而且有两个

注:以上方法虽然能够得到答案,但其理由可信度不高,故无法给满分.
法二:由OP⊥OQ得
θ+2
•2
sinθ=0,即πθ=-24sinθ(π<θ<2π),
由此作出函数y=πx(π<x<2π)及y=-24sinx(π<x<2π)图象,由图象可知满足条件的Q点有两个.

注:数形结合是我们解题中常用的方法,但就其严密性而言,仍有欠缺和不足.
法三:由OP⊥OQ得
θ+2
•2
sinθ=0,即πθ+24sinθ=0(π<θ<2π),问题转化为研讨函数h(x)=πx+24sinx(π<x<2π)零点个数.
∵h'(x)=π+24cosx,h''(x)=-24sinx
当π<x<2π时,h''(x)>0恒成立,从而说明函数h'(x)在(π,2π)中是单调递增函数,
又h'(π)<0,h'(2π)>0故存在θ0∈(π,2π),使得h'(θ0)=0,
从而函数h(x)在区间(π,θ0)单调递减,在区间(θ0,2π)单调递增,
又h(π)>0,h(2π)>0,h(
π)<0,由零点存在定理得函数h(x)在区间(π,
)和区间(
,2π)上各有一个零点.
注:该方法解题严密,但对学生数学素养要求较高.本题还有其他不少做法,大家可以再去研讨.
| 3 |
| ωx |
| 2 |
| ωx |
| 2 |
| 3 |
=2
| 3 |
| π |
| 3 |
∵A为图象的最高点,∴A的纵坐标为2
| 3 |
又∵△ABC为正三角形,所以|BC|=4
∴
| T |
| 2 |
| 2π |
| ω |
| π |
| 4 |
∴f(x)=2
| 3 |
| π |
| 4 |
| π |
| 3 |
(2)由题意可得g(x)=2
| 3 |
| π |
| 2 |
| 3 |
法一:作出如右图象,由图象可知满足条件的点Q是存在的,而且有两个

注:以上方法虽然能够得到答案,但其理由可信度不高,故无法给满分.
法二:由OP⊥OQ得
| π |
| 2 |
| 3 |
| 3 |
由此作出函数y=πx(π<x<2π)及y=-24sinx(π<x<2π)图象,由图象可知满足条件的Q点有两个.

注:数形结合是我们解题中常用的方法,但就其严密性而言,仍有欠缺和不足.
法三:由OP⊥OQ得
| π |
| 2 |
| 3 |
| 3 |
∵h'(x)=π+24cosx,h''(x)=-24sinx
当π<x<2π时,h''(x)>0恒成立,从而说明函数h'(x)在(π,2π)中是单调递增函数,
又h'(π)<0,h'(2π)>0故存在θ0∈(π,2π),使得h'(θ0)=0,
从而函数h(x)在区间(π,θ0)单调递减,在区间(θ0,2π)单调递增,
又h(π)>0,h(2π)>0,h(
| 3 |
| 2 |
| 3π |
| 2 |
| 3π |
| 2 |
注:该方法解题严密,但对学生数学素养要求较高.本题还有其他不少做法,大家可以再去研讨.
点评:本题主要考察了三角函数中的恒等变换应用,函数y=Asin(ωx+φ)的图象变换,考察了数形结合,属于中档题.

练习册系列答案
相关题目
 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E、F分别为A1C1、BC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E、F分别为A1C1、BC的中点. 如图所示,正方形ADEF与梯形ABCD所在平面互相垂直,在梯形ABCD中,AB∥CD,△ABD和△DBC分别是以DB和CD为斜边的等腰直角三角形,AD=1.
如图所示,正方形ADEF与梯形ABCD所在平面互相垂直,在梯形ABCD中,AB∥CD,△ABD和△DBC分别是以DB和CD为斜边的等腰直角三角形,AD=1.